Previous: 10.23 Модель машины конечных состояний    UP: 10 Приложения     Next: 10.25 Интернет вчера, сегодня и завтра

10.24 Сети Петри

Семенов Ю.А. (ИТЭФ-МФТИ)
Yu. Semenov (ITEP-MIPT)

Протоколы можно описывать не только с помощью модели машины конечных состояний. Альтернативой можно считать сети Петри (смотри, также книгу "Сети Петри", Котов В.Е., Москва, "Наука", ГРФМЛ, 1984 откуда взяты некоторые примеры и фрагменты данной статьи). Модель сети Петри является принципиально асинхронной и служит для отображения и анализа причинно-следственных связей в системе. Для привязки к определенным моментам времени тех или иных переходов в синхронных системах используются события. Переходы из состояния в состояния считаются "мгновенными". Если переход реально происходит через какие-то промежуточные состояния, а нам существенно учесть в модели эти обстоятельства, то вводятся соответствующие "подсобытия". Сеть Петри имеет четыре базовых элемента: позиции (places), переходы, дуги и метки (token).

Позиция (место) - это состояние, в котором находится система или определенная ее часть. Смотри рис. 10.24.1.

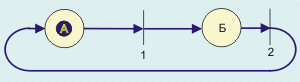
Рис. 10.24.1. Сеть Петри с двумя позициями и двумя переходами. Цифрами 1 и 2 обозначены переходы, а буквами А и Б - позиции.

Состояние системы формируется в результате реализации локальных операций, называемых условиями реализации событий. Условие имеет емкость:

• Условие не выполнено - емкость равна нулю
• Условие выполнено - емкость равна 1.
• Условие выполнено с n-кратным запасом - емкость равна n.

Определенная комбинация условий может стимулировать определенное событие, которое вызовет в свою очередь изменение изменение условий. В сетях Петри события и условия отображаются абстрактными символами, называемыми переходами(вертикальными или горизонатальными полосками - "барьерами") и позициями (кружками). Условия-позиции и события-переходы связаны отношениями зависимости, которые отображаются с помощью ориентированных дуг. Позиции, из которых исходят дуги данного перехода, называются входными позициями. Позиции же, к которым ведут дуги данного перехода, называются выходными позициями. Выполнение условий отображается помещением соотвествтующего числа меток в соответствующую позицию. Если число меток велико (более 2-3), емкость условия может быть отображена числом.

В исходный момент система находится в состоянии А, что отмечено на рис. 4.9. меткой в виде синего кружочка. Переходы обозначаются горизонтальными или вертикальными линиями. Каждый переход имеет нуль или более входных дуг, исходящих из позиций, и нуль или более исходящих дуг, направленных к выходным позициям. Переход разрешен, если имеется как минимум одна входая метка в каждой из его исходных позиций. Любой разрешенный переход может произойти (fire), удалив все входные метки и установив метки в выходных позициях, что отражает изменение условий (и емкостей). Если числа входных и выходных дуг отличаются, число меток не сохраняется. Если разрешено более одного перехода, может произойти любой из них. Причем один из осуществившихся переходов, может блокировать реализацию всех остальных переходов из данного набора. Формализм сетей Петри не предусматривает каких-либо механизмов преодоления подобных конфликтов. Переход осуществляется, если выполнены все условия реализации данного события. Если два или более переходов могут осуществиться (выполнены все условия) и они не имеют общих входных позиций, то из реализация некоррелирована и может происходить параллельно или в любой последовательности. Выбор перехода, вообще говоря, не определен. В отличии от модели машины конечных состояний здесь отсутствуют комбинированные состояния типа отправитель-канал-получатель, и переходы из состояния в состояние для каждого процесса или объекта рассматриваются независимо. Если условия ни для одного из переходов не реализованы, сеть переходит в заблокированное состояние.

Аналитическое определение. Сеть Петри - набор N = (P, T, F, W, M₀), где (P, T, F) - конечная сеть (множество Х = З u T конечно), а W: F→ N\ {O} (знак \ здесь означает разность множеств) и M₀: P→N - две функции, называемые кратностью дуг и начальной пометкой. Первая ставит в соответствие каждой дуге число N>0 (кратность дуги). Если N>0, то при графическом представлении сети число N выписывается рядом с короткой чертой, пересекающей дугу. Дуги с кратностью 1 не помечаются. Каждой позиции p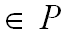 ставится в соответствие некоторое число M₀(p) 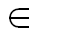N (пометка позиции).

Формально работа сети Петри описывается множеством последовательностей срабатываний и множеством реализуемых разметок позиций.

Для сетей Петри существует удобная алгебраическая нотация. Каждому переходу ставится в соответствие правило грамматики. Каждое правило специфицирует входную и выходную позиции. Текущее состояние сети Петри характеризуется неупорядоченным набором позиций. Каждая позиция присутствует в этом наборе столько раз, сколько меток она имеет.