Previous: 2.6.4 Метод Шеннона-Фано
UP:
2.6 Методы сжатия информации |
Previous: 2.6.4 Метод Шеннона-Фано
UP:
2.6 Методы сжатия информации |
2.6.5 Статический алгоритм Хафмана
Семенов Ю.А. (ГНЦ ИТЭФ)
Статический алгоритм Хафмана можно считать классическим (см. также Р. Галлагер. Теория информации и надежная связь. “Советское радио”, Москва, 1974.) Определение статический в данном случае относится к используемым словарям. Смотри также www.ics.ics.uci.edu/~dan/pubs/DataCompression.html (Debra A. Lelewer и Daniel S. Hirschberg).
Пусть сообщения m(1),…,m(n) имеют вероятности P(m(1)),… P(m(n)) и пусть для определенности они упорядочены так, что P(m(1)) і P(m(2)) і … і P(m(N)). Пусть x1,…, xn – совокупность двоичных кодов и пусть l1, l2,…, lN – длины этих кодов. Задачей алгоритма является установление соответствия между m(i) и xj. Можно показать, что для любого ансамбля сообщений с полным числом более 2 существует двоичный код, в котором два наименее вероятных кода xN и xN-1 имеют одну и ту же длину и отличаются лишь последним символом: xN имеет последний бит 1, а xN-1 – 0. Редуцированный ансамбль будет иметь свои два наименее вероятные сообщения, сгруппированными вместе. После этого можно получить новый редуцированный ансамбль и так далее. Процедура может быть продолжена до тех пор, пока в очередном ансамбле не останется только два сообщения. Процедура реализации алгоритма сводится к следующему (см. рис. 2.6.5.1). Сначала группируются два наименее вероятные сообщения, предпоследнему сообщению ставится в соответствие код с младшим битом, равным нулю, а последнему – код с единичным младшим битом (на рисунке m(4) и m(5)). Вероятности этих двух сообщений складываются, после чего ищутся два наименее вероятные сообщения во вновь полученном ансамбле (m(3) и m`(4); p(m`(4)) = p(m(4)) + P(m(5))).
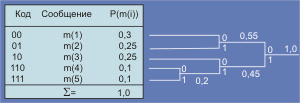
Рис. 2.6.5.1 Пример реализации алгоритма Хафмана
На следующем шаге наименее вероятными сообщениями окажутся m(1) и m(2). Кодовые слова на полученном дереве считываются справа налево. Алгоритм выдает оптимальный код (минимальная избыточность).
Но при использовании кодов разной длины могут возникнуть проблема разделение кодовых слов при последовательной пересылке. Например [6], пусть <(a,1); (b,01); (c,101); (d,011)>, тогда битовая последовательность 1011 может быть интерпретирована как aba, ca или ada. Чтобы избежать этой неопределенности можно посылать код длины перед каждым символом, что связано с пересылкой дополнительных данных. Более эффективным решением является конструирование кодов, в которых мы можем всегда однозначно преобразовать битовую последовательность в кодовое слово. Кодом такого типа является префиксный код, в котором никакая битовая строка не является префиксом другого кода. Например, <(a,1); (b.01);(c,000);(d,001)>. Префиксные коды имеют то преимущество перед другими кодами, что мы можем дешифровать любое сообщение без необходимости выявления начала следующего. Префиксный код может быть представлен в виде двоичного дерева:
Такое дерево называется деревом префиксных кодов. Это дерево может использоваться и при декодировании префиксных кодов. При поступлении битов декодер может следовать вдоль дерева, пока не достигнет листа, формируя таким способом сообщение. После этого при поступлении очередного бита осуществляется возврат к корню дерева и процедура повторяется. При декодировании могут использоваться несколько префиксных деревьев.
При использовании кодирования по схеме Хафмана надо вместе с закодированным текстом передать соответствующий алфавит. При передаче больших фрагментов избыточность, сопряженная с этим не может быть значительной. Для одного и того же массива бит могут быть сформированы разные алфавиты, но они будут одинаково оптимальными (среднее число бит, приходящихся на один символ для любого такого алфавита, будет идентичным). Таким образом, коды Хафмана являются оптимальным (наиболее экономным), но не единственным решением.
Возможно применение стандартных алфавитов (кодовых таблиц) для пересылки английского, русского, французского и т.д. текстов, программных текстов на С++, Паскале и т.д. Кодирование при этом не будет оптимальным, но исключается статистическая обработка пересылаемых фрагментов и отпадает необходимость пересылки кодовых таблиц. Ниже в таблице представлена таблица возможных кодов Хафмана для английского алфавита.
| Буква | Код Хафмана |
| E | 100 |
| T | 001 |
| A | 1111 |
| O | 1110 |
| N | 1100 |
| R | 1011 |
| I | 1010 |
| S | 0110 |
| H | 0101 |
| D | 11011 |
| L | 01111 |
| F | 01000 |
| C | 01000 |
| M | 00011 |
| U | 00010 |
| G | 00001 |
| Y | 00000 |
| P | 110101 |
| W | 011101 |
| B | 011100 |
| V | 1101001 |
| K | 110100011 |
| X | 110100001 |
| J | 110100000 |
| Q | 1101000101 |
| Z | 1101000100 |
Ниже представлена аналогичная таблица для русского алфавита [Яглом А.М., Яглом И.М. "Вероятность и информация". 3-е изд. - Наука, 1973]. В этой таблице коды букв Е и Ё идентичны, аналогичная сутуация с кодами Ь и Ъ. Следует также иметь в виду, что помимо букв определенные коды должны быть присвоены символам пунктуации, числам и некоторым специальным символам (1 2 3 4 5 6 7 8 9 0 . , : ; ! ? ... ' " ~ % # * + - = \ ( ) [ ] { } _).
| Буква | Относит. частота |
Код Хафмана |
| – пробел | 0,175 | 111 |
| O | 0,090 | 110 |
| Е,Ё | 0,072 | 1001 |
| А | 0,062 | 1010 |
| И | 0,062 | 1001 |
| T | 0,053 | 1000 |
| Н | 0,053 | 0111 |
| C | 0,045 | 0110 |
| Р | 0,040 | 01011 |
| В | 0,038 | 01010 |
| Л | 0,035 | 01001 |
| К | 0,028 | 01000 |
| М | 0,026 | 00111 |
| Д | 0,025 | 001101 |
| П | 0,023 | 001100 |
| У | 0,021 | 00101 |
| Я | 0,018 | 001001 |
| Ы | 0,016 | 001000 |
| З | 0,016 | 000111 |
| Ь,Ъ | 0,014 | 000110 |
| Б | 0,014 | 000101 |
| Г | 0,013 | 000100 |
| Ч | 0,012 | 000011 |
| Й | 0,010 | 0000101 |
| Х | 0,009 | 0000100 |
| Ж | 0,007 | 0000011 |
| Ш | 0,006 | 00000101 |
| Ю | 0,006 | 00000100 |
| Ц | 0,004 | 00000010 |
| Щ | 0,003 | 00000001 |
| Э | 0,003 | 000000001 |
| Ф | 0,002 | 000000000 |
Возможная схема реализации алгоритма формирования кодов Хафмана для русского алфавита показана на рис. 2.6.5.2.
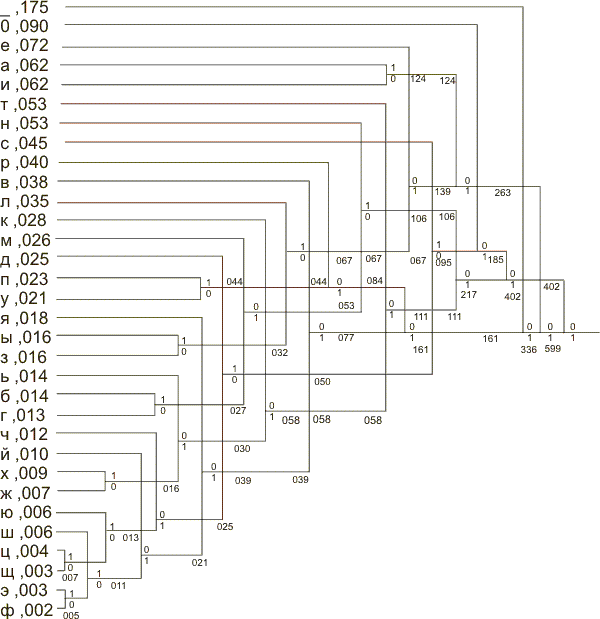
Рис. 2.6.5.2
Среднее число элементарных сигналов для передачи буквы при данном методе кодирования равно 4,4.
| Следует заметить, что часто встречающиеся символы (последовательности бит) несут меньше информации, чем редко встречающиеся, не случайно для них применено большее число бит. Также как поезд, сходящий с рельс, имеет большую информационную емкость, чем поезд прибывающий по расписанию. Не случайно люди интуитивно воспринимают сообщения о несчастьях с большим интересом. |
Previous: 2.6.4 Метод Шеннона-Фано
UP:
2.6 Методы сжатия информации |