Previous: 3.6 Протокол G.703    UP: 3 Каналы передачи данных

3.7 Дерево Штайнера

Семенов Ю.А. (ИТЭФ-МФТИ)
Yu. Semenov (ITEP-MIPT)

Алгоритм дерева Штайнера используется в телекоммуникациях при оптимизации маршрутов передачи мультимедийных данных. Рассмотрим проблему поиска оптимального пути в предположении, что критерием оптимизации является длина этого пути. Задача может быть решена следующим образом:

1. Сначала находим два ближайших узла. Если соединение их не создаст циклических путей, производим такое объединение.
2. Повторяем операцию до тех пор, пока не будут объединены все узлы.

Алгоритм может быть упрощен. Сначала пометим все узлы уникальным образом. Затем находим два ближайшие узла с разными метками и соединяем их. После этого оба узла получают идентичные метки. Когда все узлы окажутся соединенными, они все получат идентичные метки. Имеется возможность добавления к графу дополнительных виртуальных точек Штайнера (1В), которые могут позволить сократить суммарную длину соединений. Смотри рис. 1 (http://www.colorstudy.com/static/ianb/old/steiner/summary.html; а также D. M. Warm, P. Winter, M. Zachariasen. Exact Algorithms for Plane Steiner Tree Problems: Computational Study, Advances in Steiner Trees, pages 81-116, Kluwer Academic Publishers, 2000; http://www.diku.dk/users/martinz/#publications).

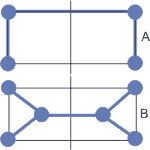
Рис.1. Пример уменьшения суммарной длины дерева путем введения дополнительных точек

Метрика дерева варианта А равна 4 (длина ребра ячейки имеет метрику 1), а варианта В 1+4*sqrt(1/2)=3,83. Вариант В на рисунке 1 не всегда реализуем, так как в некоторых случаях узлы Штайнера могут иметь только целочисленные координаты (х,у), тогда точки Штайнера не могут сократить длину соединений для графа на рис. 1. В этом варианте расстояние между узлами (x1,y1) и (x2,y2) равно abs(x1-x2)+abs(y1-y2). Пример использования точек Штайнера для такого варианта показан на рис. 2.

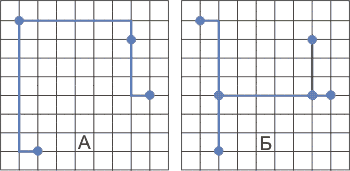
Рис. 2. Использование точек Штайнера для минимизации длины маршрута по ортогональной сетке

Дерево варианта А на рис. 2 характеризуется метрикой 19, а для Б после добавления двух точек Штайнера (выделены более светлой закраской) метрика равна 17.

Довольно часто (телекоммуникации, а также трассировка печатных плат и микросхем) приходится сталкиваться с проблемами поиска оптимальных деревьев Штайнера в плоскости (Эвклида и прямолинейный).

Проблема сводится к поиску наикратчайшей длины дерева Штайнера SMT (Shortest Minimum Tree). При этом приходится размещать набор из n терминалов на плоскости с учетом эвклидовой L₂-метрики и/или прямолинейной (или Манхэттеновской) L₁-метрики.

Пусть u=(u_x,u_y) и v=(v_x,v_y) являются парой точек на декартовой плоскости Â. Расстояние между этими точками в метрике L_p (L_p -расстояние, 1 £ p £ ¥) характеризуется 2uv2_p= (|u_x - v_y|^p + |u_x - v_y|^p)^1/p.

Эвклидовские SMT (ESMT) и прямолинейные SMT (RSMT) представляют собой подмножества полных деревьев Штайнера (FST). Эвклидово FST (EFST) и прямолинейное FST (RFST), охватывающие k терминалов, 2£ k £ n, имеет k-2 точек Штайнера (за исключением случая k=4; RFST могут тогда иметь одну точку Штайнера с четырьмя исходящими ребрами). Точки Штайнера в EFST имеют три исходящих ребра. Точки Штайнера в RSMT имеют также три исходящих ребра (за исключением выше приведенного случая). Длина EMST (соответственно RMST) превосходит длину ESMT (соответственно RSMT) как минимум в 2/Ö3 раз (соответственно 3/2 раз) [смотри F. K. Hwang, D. S. Richards and P. Winter. The Steiner Tree Problem. Annals of Discrete Mathematics 53. Elsevier Science Publishers, Netherlands, 1992.].

При поиске SMT для эвклидова или прямолинейного варианта субнаборы терминалов рассматриваются один за другим. Для каждого субнабора определяются все его FST один за другим. Кратчайшие из них запоминаются. Узким местом данного подхода является формирование FST.