Quantum computing is one of those technologies that’s so arcane that TV characters name drop it when they want to sound smart.

Quantum computing as an idea has been around for a while — the theoretical possibility was originally introduced by Yuri Manin and Richard Feynman in 1982.  Over the last few years, though, the field has been edging worryingly closer to practicality.

Companies like Google and Microsoft, as well as government agencies like the NSA have all been feverishly pursuing quantum computers for years now.  A company called D-Wave has produced and is selling devices that (while they aren’t proper computers, and can only perform a few algorithms) exploit quantum properties, and are another incremental step on the road toward a fully Turing-complete quantum machine. What Is The Turing Test And Will It Ever Be Beaten? What Is The Turing Test And Will It Ever Be Beaten? The Turing Test is meant to determine whether machines think. Did the Eugene Goostman program truly pass the Turing test, or did the creators simply cheat? Read More

It doesn’t seem unreasonable to say that breakthroughs might occur that will allow the first large-scale quantum computer to be built within a decade.

So why all the interest?  Why should you care?  Computers get faster all the time – what’s so special about quantum computers? What Is Moore's Law, And What Does It Have To Do With You? [MakeUseOf Explains] What Is Moore's Law, And What Does It Have To Do With You? [MakeUseOf Explains] Bad luck has nothing to do with Moore's Law. If that is the association you had, you are confusing it with Murphy's Law. However, you were not far off because Moore's Law and Murphy's Law... Read More

In order to explain why these machines are so important, we’re going to have to take a step back and explore exactly what quantum computers are, and why they work.  To start off, let’s talk about a concept called “runtime complexity.”

What is Runtime Complexity?

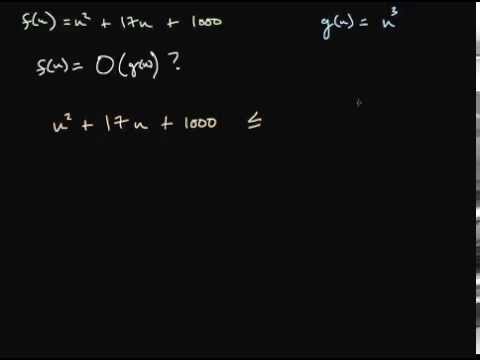
One of the big surprises in the early days of computer science was the discovery that, if you have a computer that solves a problem of a certain size in a certain amount of time, doubling the speed of the computer does not necessarily let it tackle problems twice as big.

Some algorithms increase in total execution time very, very quickly as the size of the problem grows – some algorithms can be rapidly completed given 100 data points, but completing the algorithm given 1000 data points would require a computer the size of the Earth running for a billion years.  Runtime complexity is a formalization of this idea: it looks at the curve of how fast the complexity of a problem grows, and uses the shape of that curve to classify the algorithm.

Generally, these classes of difficulty are expressed as functions.  An algorithm that gets proportionately harder when the data set its working on increases (like a simple counting function) is said to be a function with a runtime complexity of “n” (as in, it takes n units of time to process n data points).

Alternately, it might be called “linear”, because when you graph it, you get a straight line.  Other functions might be n^2 or 2^n or n! (n factorial).  These are polynomial and exponential.  In the latter two cases, the exponential ones grow so quickly that in almost all cases they can’t be solved for anything except very trivial examples.

Runtime Complexity and Cryptography

If you’re hearing this stuff for the first time and it sounds meaningless and arcane, let’s try to ground this discussion.  Runtime complexity is critical for cryptography, which relies on making decryption much easier for people who know a secret key than for those who don’t.  In an ideal cryptographic scheme, decryption should be linear if you have the key, and 2^k (where k is the number of bits in the key) if you don’t.

In other words, the best algorithm for decrypting the message without the key ought to be simply guessing possible keys, which is intractable for keys only a few hundred bits long.

For symmetric key cryptography (in which the two parties have the chance to exchange a secret securely before they start communication) this is pretty easy.  For asymmetric cryptography, it’s harder.

Asymmetric cryptography, in which the encryption and decryption keys are different and can’t be easily computed from one another, is a much harder mathematical structure to implement than symmetric cryptography, but it’s also a lot more powerful: asymmetric crypto lets you have private conversations, even over tapped lines!  It also allows you to create “digital signatures” to allow you to verify who a message came from, and that it hasn’t been tampered with.

These are powerful tools, and make up the foundation of modern privacy: without asymmetric cryptography, users of electronic devices would have no reliable protection against prying eyes.

Because asymmetric cryptography is harder to build than symmetric, the standard encryption schemes that are in use today are not as strong as they could be: the most common encryption standard, RSA, can be cracked if you can efficiently find the prime factors of a very large number.  The good news is that that’s a very hard problem.

The best known algorithm for factoring large numbers into their component primes is called the general number field sieve, and has a runtime complexity that grows a little slower than 2^n.  As a consequence, keys have to be about ten times longer in order to provide similar security, which is something that people normally tolerate as a cost of doing business.  The bad news is that the entire playing field changes when quantum computers get thrown into the mix.

Quantum Computers: Changing the Crypto Game

Quantum computers work because they can have multiple internal states at the same time, through a quantum phenomenon called “superposition”.  That means that they can attack different parts of a problem simultaneously, split across possible versions of the universe.  They can also be configured such that the branches that solve the problem wind up with the most amplitude, so that when you open the box on Schrodinger’s cat, the version of the internal state that you’re most likely to be presented with is a smug-looking cat holding a decrypted message.

For more information about quantum computers, check out our recent article on the subject! How do Optical and Quantum Computers work? How do Optical and Quantum Computers work? The Exascale Age is coming. Do you know how optical and quantum computers work, and will these new technologies become our future? Read More

The upshot of this is that quantum computers aren’t just linearly faster, the way normal computers are: getting two or ten or a hundred times faster doesn’t help much when it comes to conventional cryptography that you’re hundreds of billions of times too slow to process.  Quantum computers support algorithms that have smaller-growing run time complexities than are otherwise possible.  This is what makes quantum computers fundamentally different from other future computational technologies, like graphene and memrister computation.

For a concrete example, Shor’s Algorithm, which can only be executed on a quantum computer, can factor large numbers in log(n)^3 time, which is drastically better than the best classical attack.  Using the general number field sieve to factor a number with 2048 bits takes about 10^41 units of time, which works out to more than a trillion trillion trillion.  Using Shor’s algorithm, the same problem only takes about 1000 units of time.

The effect gets more pronounced the longer the keys are.  That’s the power of quantum computers.

Don’t get me wrong – quantum computers have a lot of potential non-evil uses.  Quantum computers can efficiently solve the travelling salesman problem, allowing researchers to build more efficient shipping networks and design better circuits. Quantum computers already have powerful uses in artificial intelligence.

That said, their role in cryptography is going to be catastrophic.  The encryption technologies that allow our world to keep functioning depend on the integer factorization problem being hard to solve.  RSA and related encryption schemes are what let you trust you’re on the right website, that the files you download aren’t riddled with malware, and that people aren’t spying on your Internet browsing (if you’re using Tor).

Cryptography keeps your bank account safe and secures the world’s nuclear infrastructure.  When quantum computers become practical, all of that technology stops working.  The first organization to develop a quantum computer, if the world still works on the technologies we use today, is going to be in a frighteningly powerful position.

So, is the quantum apocalypse inevitable?  Is there anything we can do about it?  As it turns out… yes.

Post-Quantum Cryptography

There are several classes of encryption algorithms that, as far as we know, are not significantly faster to solve on a quantum computer.  These are known collectively as post-quantum cryptography, and provide some hope that the world can transition to cryptosystems that will remain secure in a world of quantum encryption.

Promising candidates include lattice-based encryption, like Ring-Learning With Error, which derives its security from a demonstrably complex machine learning problem, and multivariate cryptography, which derives its security from the difficulty of solving very large systems of simple equations.  You can read more about this topic on the Wikipedia article.  Beware: a lot of this stuff is complex, and you may find that your mathematics background needs to be beefed up considerably before you can really dig into the details.

The takeaway from a lot of this is that post-quantum cryptoschemes are very cool, but also very young.  They need more work to be efficient and practical, and also to demonstrate that they are secure.  The reason that we are able to trust cryptosystems is because we’ve thrown enough clinically paranoid geniuses at them for long enough that any obvious shortcomings would have been discovered by now, and researchers have proved various characteristics that make them strong.

Modern cryptography depends on light as a disinfectant, and most of the post-quantum cryptographic schemes are simply too new to trust world security to.  They’re getting there, though, and with a little luck and some preparation, security experts can complete the switch before the first quantum computer ever comes on line.

If they fail, however, the consequences may be dire.  The thought of anyone having that kind of power is unsettling, even if you’re optimistic about their intentions.  The question of who first develops a working quantum computer is one that everyone should watch very carefully as we move into the next decade.

Are you concerned about the insecurity of cryptography to quantum computers? What’s your take? Share your thoughts in the comments below!

Image Credits: Binary orb Via Shutterstock

Email isn’t a secure medium—it comes with risks, both to your privacy and to your computer. Okay. Now that’s out of the way, we can get onto eight tips that anyone—no matter how tech savvy—can use for increasing their email security. Send them to your family, friends, colleagues, or anyone else who needs to increase their email security! Why Email Can't Be Protected From Government Surveillance Why Email Can't Be Protected From Government Surveillance “If you knew what I know about email, you might not use it either,” said the owner of secure email service Lavabit as he recently shut it down. "There is no way to do encrypted... Read More

Choose a Good Password

This should be obvious, but there are a lot of people out there who still have their kids’ names or their birthdates as their passwords. If your password is this simple, it’s not going to be hard to guess or crack using some basic software. We’ve given you advice on how to select a good password, and told you about a number of apps that can help you manage all of your passwords, so you don’t choose easy-to-remember ones.

You really have no excuse now.

Don’t Open Suspicious Emails

Again, it seems like it should go without saying, but so many of us get on autopilot when we’re going through our inboxes and open up just about everything. If an email doesn’t have a “From” name, if it comes from a weird-looking address, or if there are any other signs of it being a malicious attempt at getting you to do something (the image above is a pretty obvious example), just delete it. You never know if there will be a link or an image in it that could infect your computer.

Don’t Open Suspicious Attachments

This is related to the previous item, but bears being brought up specifically. Even if someone sends you a totally legitimate email, it’s possible that they’ve accidentally or unknowingly included a malicious attachment. If they didn’t say anything about attaching a document or a photo, or the filename doesn’t look right, don’t open it.

Opening a bad file is one of the fastest ways to infect your computer and potentially the computers of the people you’re in contact with.  This handy guide on how to spot a dangerous email attachment is a great resource for staying safe. How To Spot A Dangerous Email Attachment How To Spot A Dangerous Email Attachment Emails can be dangerous. Reading the contents of an email should be safe if you have the latest security patches, but email attachments can be harmful. Look for the common warning signs. Read More

Disable Automatic Image Loading

One of the ways that a hacker can get run malicious code on your computer is by embedding it in an image file. If your email app loads the image, it could potentially infect your computer. That’s why so many email programs allow you to disable the automatic loading of images and give you the option of loading images on individual emails. It’s rarely a hassle, and it will make your account more secure. (In Gmail, go to Settings > General > Images and select Ask before displaying external content.)

Think Before You Send

If you’re sending something that you don’t want to be released on the web, think twice about sending it. Even if you’re confident about your email security, who knows what will happen on the other end? It could be backed up, lost, forwarded, intercepted, or otherwise diverted in front of prying eyes. 5 Ways to Backup your Email 5 Ways to Backup your Email Read More

And always be sure to double-check your recipient list; in the days of auto-complete, we tend to assume that the Karen we’re sending to is the right Karen. But that’s not always the case.

Don’t Send Sensitive Information

Because it can be relatively easy to impersonate someone else using email, you shouldn’t send confidential information. Ever. Don’t send the code to your garage door to your neighbor, don’t send your social security number to your parents, don’t send your bank account information to anyone.

Even the bank.

Most reputable companies won’t ask you for sensitive information via email, so if someone’s asking for your username and password, you might be the target of a phishing attack. In almost every case, it’s safer to transmit shareable information – to a confirmed contact – via a phone call or in person. What Exactly Is Phishing & What Techniques Are Scammers Using? What Exactly Is Phishing & What Techniques Are Scammers Using? I’ve never been a fan of fishing, myself. This is mostly because of an early expedition where my cousin managed to catch two fish while I caught zip. Similar to real-life fishing, phishing scams aren’t... Read More

Think Twice about Logging In

Assuming you’ve secured your home network, logging in to your email accounts should be pretty safe. However, logging into your email account—or even just accessing the Internet—on public wi-fi or from a public computer can be a risk. We’re all guilty of it, but it pays to be cognizant of your surroundings—if you’re in an especially dodgy Internet cafe or on totally unsecured wi-fi, don’t sign in unless you need to. WPA2, WEP, And Friends: What's The Best Way To Encrypt Your Wi-Fi? WPA2, WEP, And Friends: What's The Best Way To Encrypt Your Wi-Fi? When setting up wireless encryption on your router, you'll come across a variety of confusing terms -- WPA2, WPA, WEP, WPA-Personal, and WPA-Enterprise. Read More

Enable Two-Factor Authentication

Up to this point, we’ve stuck with the most basic security tips that can be accomplished with a minimal amount of effort. This final tip requires a bit more work, but can make a huge difference in the security level of your email account. And while you’re at it, add two-factor authentication to as many other services as you can.

If you’re not sure about whether or not you want to go through the extra effort, check out these four ways to make two-factor authentication easier. Can Two-Step Verification Be Less Irritating? Four Secret Hacks Guaranteed to Improve Security Can Two-Step Verification Be Less Irritating? Four Secret Hacks Guaranteed to Improve Security Do you want bullet-proof account security? I highly suggest enabling what's called "two-factor" authentication. Read More

Only You Can Prevent Email Security Breaches

There are plenty of complicated and technologically advanced steps that you can take to secure your email (like encrypting with PGP), but not everyone is willing to invest the time to be that safe. The eight tips above, however, are simple and easy to put in place, so share them with your colleagues, friends, and family to help them stay safe online! PGP Me: Pretty Good Privacy Explained PGP Me: Pretty Good Privacy Explained Read More

What have we missed here? What are other good ways to stay safe when it comes to email security?

Image credits: Login or sign in form with username and password fields. via Shutterstock.