Previous: 10.31 Семантические сети
UP:
10 Приложения |
Previous: 10.31 Семантические сети
UP:
10 Приложения |
10.32 Практические формулы и методы обработки результатов измерений
Семенов Ю.А. (ГНЦ ИТЭФ)
Приведенные здесь данные часто не подтверждаются доказательствами даже в тех случаях, когда такие доказательства достаточно просты. Определяющим принципом подбора материала была простота использования и удовлетворительная с практической точки зрения точность. Это краткий справочник, а не учебник. Примером учебника по этой теме можно считать книгу Д.Хадсона "Статистика для физиков" (изд. Мир, доступна в Интернет). Предполагается, что читатель имеет представление о вероятности, функции плотности вероятности, дисперсии и наиболее вероятном значении.
Предполагается, что если мы измеряем величину a=a*±Da
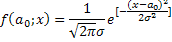 | (1) |
где a0 - наиболее вероятное среднее значение, а σ - среднеквадратичное отклонение.
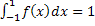 (условие нормировки)
(условие нормировки)
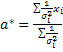 | (2) |
Если ошибки измерения одинаковы, то a*:
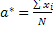 , где N – число измерений, а xi – измерение с номером i.
, где N – число измерений, а xi – измерение с номером i.
Хотя формула (2) получена в предположении, что хi имеет Гауссово распределение, результат слабо зависит от формы распределения (лишь бы дисперсия была конечна).
Наиболее вероятная ошибка величины a (Da)(среднеквадратичное отклонение):
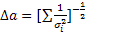 | (3) |
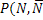 ) = ) = 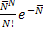 | (4) |
Здесь – среднее значение 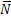 , а среднеквадратичное значение ошибки измерения N равно
, а среднеквадратичное значение ошибки измерения N равно 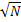 .
.
Рассмотрим случай, когда событие может быть отнесено к одному из двух классов (верх-низ; вперед-назад; +/-; орел-решка). Пусть p – вероятность попадания события в класс 1.Тогда вероятность попадания в класс 2 равна (1-р).
Суммарная вероятность наблюдения N1 событий класса 1 из общего числа N будет подчиняться биномиальному распределению:
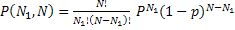 | (5) |
При этом 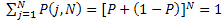 (предполагается, что нам безразличен порядок событий).
(предполагается, что нам безразличен порядок событий).
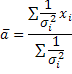 , , | (6) |
где si - среднеквадратичная ошибка результата измерения xi.
Коэффициент корреляции результатов измерения x1 и x2 (ковариация) вычисляется по формуле (значения x с чертой - усредненное значение результата измерения):
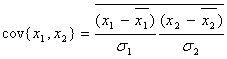 , , | (7) |
где si - среднеквадратичная ошибка результата измерения xi. x1 и x2 могут быть величинами разными по своей природе и иметь разную размерность.
Если некоторая физическая величина Y является функцией от a (Y=Y(a1,… aM)), то
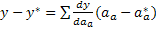 | (8) |
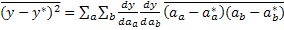 | (9) |
Частным случаем уравнения (9), справедливым, когда переменные не коррелированны, является:
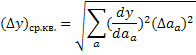 | (10) |
Следует иметь в виду, что ошибкой суммы случайных величин A+B и разности A-B будет sA+sB,
что иногда называют "накоплением ошибки", что особенно плохо, когда А и В имеют близкие значения. Ошибка же среднего для N измерений будет в 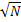 раз меньше ошибки однократного измерения.
раз меньше ошибки однократного измерения.
Довольно часто приходится решать задачу определения вида статистической функции по набору результатов измерения. Пусть Y(xi) набор таких измерений (результат измерения для значения исходного параметра xi. Предполагается, что параметр х известен без ошибки), а Y(xi) имеют среднеквадратичные ошибки si (i принимает значения от 1 до N). В качестве х могут, например, использоваться геометрические координаты, время, температура и т.д. Предположим также, что мы для проверки выбираем функцию F(x), которая характеризуется k параметрами. Если эта функция полином, то при N=k параметры будут определяться однозначно из решения системы k уравнений. Такое решение сильно зависит от статистических флуктуаций исходных измерений (неустойчиво, и не учитывает индивидуальных статистических ошибок конкретных результатов измерений). Обычно N>k, а разница N-k называется числом степеней свободы.
В случае применения критерия χ2 формируется квадратичная форма вида χ2 = s{[F(xi)-Y(xi)]2}. При этом следует помнить, что только значения Yi являются независимыми (нет корреляции) и имеют некоторое статистическое распределение, а F – является функцией, лишенной каких-либо ошибок. При наличии корреляций, данные следует сначала ортогонализовать (преобразование, исключающее корреляцию). В теории распределение Y должно быть Гауссовым, но большинство практических результатов слабо зависят от типа распределения Y.
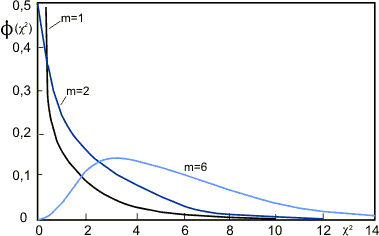
Рис. 1. χ2-распределение для различных значений степеней свободы m
χ2-распределение является частным случаем Г-распределения [2].
χ2 вычисляется по формуле 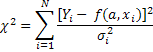 , где Yi -
результаты измерений c их среднеквадратичными ошибками si, а f(a,x,i) - аппроксимирующая функция с параметрами a.
Если число этих параметров равно m, то число степеней свободы χ2-распределения равно N-m.
, где Yi -
результаты измерений c их среднеквадратичными ошибками si, а f(a,x,i) - аппроксимирующая функция с параметрами a.
Если число этих параметров равно m, то число степеней свободы χ2-распределения равно N-m.
Функция распределения вероятности для χ2 имеет вид:
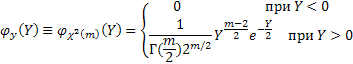
Среднее значение для этого распределения равно N-m, а среднеквадратичное отклонение DM=SQRT[2(N-m)], где N - число экспериментальных точек, а m - число искомых параметров.
Таблицы оценки достоверности той или иной гипотезы (набора параметров аппроксимирующей функции) содержат в себе вероятности:
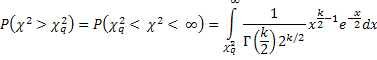 | (11) |
Для числа степеней свободы больше 2, графически это можно представить следующим образом.
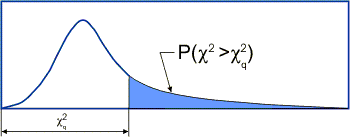
Рис. 2
Если для некоторого набора параметров мы получили значение χ2, которое существенно больше числа степеней свободы, есть все основания полагать, что данная гипотеза маловероятна. Ее вероятность можно будет определить из таблиц (11) на основе полученного значения χ2 при заданном числе степеней свободы.
Если l=l(a) была выбрана в качестве физического параметра, то тот же самый доверительный интервал будет:
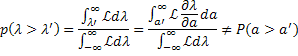
Таким образом, в общем случае численная величина доверительного интервала зависит от выбора физического параметра, при этом переход от одного параметра к другому следует выполнять согласно:
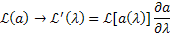
Это справедливо и для вычисления Da. Только максимально правдоподобное решение и относительные вероятности не зависят от выбора а. Для гауссовских распределений доверительные интервалы могут быть найдены с помощью таблиц интеграла вероятности.
М.С.Бартлет ввел функцию S(a), которая всегда имеет среднее равное нулю и стандартное отклонение равное 1, независимо от выбора a.
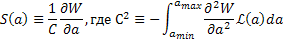
Для L(a), которая представляет собой кривую Гаусса со стандартным отклонением Da, S(a) будет:
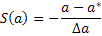
Бартлет предлагает, что поскольку распределение S больше похоже на распределение Гаусса, то 68,3%-ый доверительный интервал (одно стандартное отклонение) может быть получен путем решения для двух величин а, что дает S(a)=±2 и S(a*)=-1.
Подобным же образом доверительный интервал для отклонения в пределах двух стандартов получается путем решения S(a)=±2. Теперь покажем, что 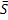 =0 и
=0 и
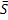 2=1
2=1
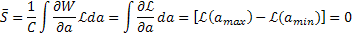
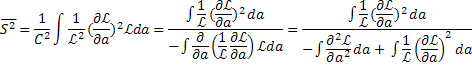
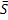 2=1, поскольку член
2=1, поскольку член
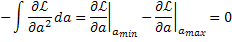
Пусть имеется N результатов измерений при значениях некоторого параметра x1,...xN (например, координат или времени).
Мы имеем результаты этих измерений в виде (y1 ±s1), ...,
yN ±sN) И пусть каждое измерение содержит Pi событий. Тогда yi=Ni
и Ni распределены по Пуассону с si=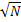 i.
i.
Пусть также, что нам нужно сопоставить наши экспериментальные данные c функцией f(ai,x).
Чтобы найти параметры функции ai минимизируем сумму среднеквадратичных отличий экспериментальных значений yi и f(ai,x).
Для этой цели формируем квадратичную форму 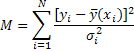 и пытаемся найти минимум М. Решения аi=a*i определяются путем нахождения минимума М. Записываем условие минимума М - ∂M/∂ai=0. Минимальное значение М называется суммой наименьших квадратов М*. Величины аi,
по которым производится минимизация M, называются решениями наименьших квадратов (коэффициентами регрессии).
и пытаемся найти минимум М. Решения аi=a*i определяются путем нахождения минимума М. Записываем условие минимума М - ∂M/∂ai=0. Минимальное значение М называется суммой наименьших квадратов М*. Величины аi,
по которым производится минимизация M, называются решениями наименьших квадратов (коэффициентами регрессии).
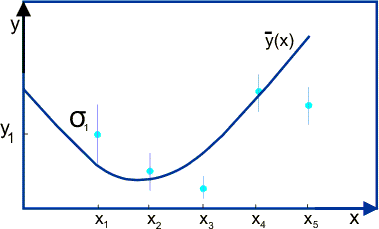
Рис. 3.
Ошибки наименьших квадратов характеризуются ниже следующим соотношением.
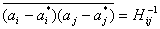 , где
, где 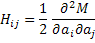 , где Hij является матрицей, а H-1 - обратная матрица для Hij.
, где Hij является матрицей, а H-1 - обратная матрица для Hij.
В матричном виде решение может быть записано в матричном виде:
a*=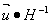 | (12) |
где u является вектором вида:
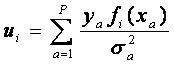 , где p - число параметров апроксимирующей функции. P должно быть меньше N. При P=N функция пройдет через все экспериментальные точки, что является тривиальным результатом. Для выбора оптимального p может быть применен критерий χ2.
, где p - число параметров апроксимирующей функции. P должно быть меньше N. При P=N функция пройдет через все экспериментальные точки, что является тривиальным результатом. Для выбора оптимального p может быть применен критерий χ2.
Рассмотрим частный случай, когда 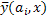 линейна по ai (случай полиномиальной аппроксимации).
линейна по ai (случай полиномиальной аппроксимации).
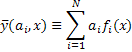
Проведя дифференцирование квадратичной формы по искомым параметрам, и приравняв результат нулю, получим число уравнений, соответствующее числу параметров. Решив эту систему уравнений можно получить искомые параметры аппроксимирующей функции.
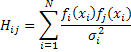
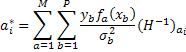
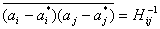 , где , где 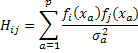 | (13) |
Уравнение (12) является полной процедурой для вычисления решений для задачи метода наименьших квадратов.
Предположим для конкретности, что функция f(a,x) является параболой,
то есть 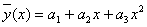 . f1=1, f2=x, а f3=x2.
. f1=1, f2=x, а f3=x2.
Пусть Х=-0,6; -0,2; 0,2 и 0,6, а результаты измерения 5±2; 3±1; 5±1; и 8±2.
При этом элементы матрицы Hij будут иметь вид.
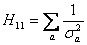
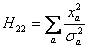
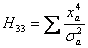
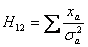
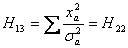
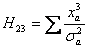
Теперь воспользуемся одним из известных методов обращения матриц и получаем значения элементов H-1, а из них - значения ai.
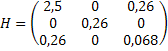
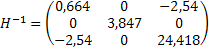
u=(11,25 0,85 1,49)
| a*1=3,685 | Da1=0,815 | 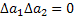 |
| a*2=3,27 | Da2=1,96 | |
| a*3=7,808 | Da3=4,96 | 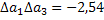 |
Da - корни квадратные из диагональных элементов H-1.
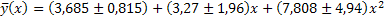 будет кривой наилучшего соответствия.
будет кривой наилучшего соответствия.
Предположим, что нам известно, что должна быть справедлива гипотеза А или гипотеза В. Если справедлива гипотеза А, то экспериментальное распределение имеет вид fA, а для гипотезы В - fB(x).
Если справедлива гипотиза А, то суммарная вероятность получения в результате отдельного опыта набора величин X1,X2,...,XN будет:
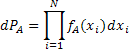
Соотношение правдоподобия R будет иметь вид:
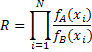
Это представляет собой вероятность того, что отдельное измерение из N событий окажется таким, как это должно быть, если справедлива гипотеза A, деленную на вероятность того, что экспериментальные данные будут такими, какими они должны быть, если справедлива гипотеза В.
Часто приходится иметь дело с бесконечным набором гипотез, т.е. с параметром, который является переменной (а). Вероятностная функция от a называется функцией правдоподобия (от английского слова Likelihood она обозначается L)
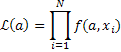 | (14) |
Функция правдоподобия есть суммарная плотность вероятности получения отдельного экспериментального результата X1,X2,...,XN, если предположить, что f(a,x) является истинной нормированной функцией распределения:
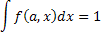
Отдельные вероятности для a могут быть представлены в виде графика зависимости функции правдоподобия от а. Величина а называется максимально-правдоподобным решением a*.
Среднеквадратичное распределение а вокруг a* является мерой точности определения а=a*. Эта мера называется Da.
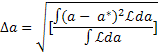 | (15) |
В общем случае функция правдоподобия будет близка к гауссовой (можно показать, что она стремится к распределению Гаусса при N → ∞) и может иметь вид, показанный ниже на рис. 4.
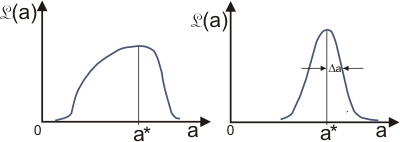
Рис. 4.
График слева является примером случая, когда имеется ограниченная статистика. В этом случае правильнее приводить форму функции правдоподобия, а не просто приводить значения a* и Da.
Когда имеется М параметров a1,a2,...,aM, которые нужно найти, способ получения максимально правдоподобного решения состоит в решении системы из М уравнений:
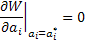 , где
, где 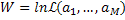
Если N велико и распределение близко к гауссову, то:
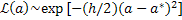 ,
,
где 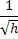 представляет собой среднеквадратичный разброс a
вокруг a*.
представляет собой среднеквадратичный разброс a
вокруг a*.
W=-(h/2)(a -a*)2 + const
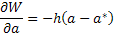
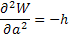
Поскольку Da, как это следует из (15), равно 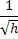 , то
, то
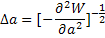 | (16) |
В случае повторных измерений ошибка может быть описана как:
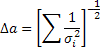 (для случая распределения Гаусса)
(для случая распределения Гаусса)
Во многих случаях оказывается невозможно аналитичиски получить выражения для a* и Da. В таких случаях кривая L(a) может быть определена численно c привлечением уравнения (14). Если L(a) не следует форме Гаусса, то лучше использовать среднее:
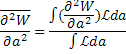
Часто бывает важно при постановке эксперимента иметь возможность заранее оценить, сколько данных необходимо для того, чтобы получить требуемую точность. Предполагается, что аппроксимирующая функция f(a,x) известна. Мы желаем знать величину ∂2W/∂2a, усредненную по большому числу повторных измерений, каждое из которых содержит N событий. Для одного события имеем:
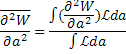
для N событий получим:
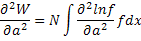
Это можно представить в форме, содержащей только первые производные, следующим образом:
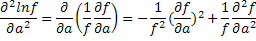
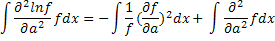
Последний интеграл обращается в нуль, если интегрирование производить до дифференцирования, так как:
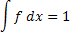
Таким образом,

и уравнение (16) приводит к выражению:
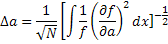 | (17) |
Если из эксперимента, состоящего из N событий должны быть определены М параметров, то формулы ошибок, приведенные выше, применены только в тех редких случаях, когда ошибки не коррелированы.
Ошибки не коррелированы, только если 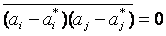 во всех случаях, когда i≠j (коэффициент корреляции равен нулю).
во всех случаях, когда i≠j (коэффициент корреляции равен нулю).
Разлагаем W(a) в окрестности a* в ряд Тейлора.

где bi ≡ ai-a*i и
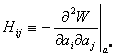 | (18) |
Второй член разложения исчезает, поскольку ¶W/¶aa=0 являются уравнениями для a*a.
ln(L(a))=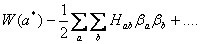
на М-мерной гауссовой поверхности. Как и прежде формулы ошибок предполагают, что L(a) подобна кривой Гаусса в области ai »a*i. Если статистика настолько мала, что такое приближение является плохим, тогда лучше приводить просто график L(a).
Согласно уравнению (18) H является симметричной матрицей. Пусть V является унитарной матрицей, которая диагонализирует H:
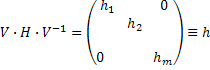 | (19) |
где 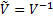
Пусть b=(b1,b2,...,bM) и g≡b× V-1, тогда элемент вероятности в b-пространстве будет:
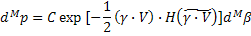
Поскольку |V|=I является якобианом, связывающим элементы объема dMb и dMg, то мы имеем:
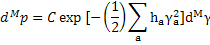
Теперь всю М-мерную гауссову поверхность следует представить в виде произведения независимых одномерных кривых Гаусса. В результате мы имеем:
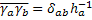
тогда 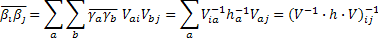
Согласно уравнению (19) H=V-1 h× V, так что окончательный результат будет:
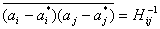 , , | (20) |
где 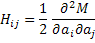
Формула усреднения по повторным экспериментам будет иметь вид:
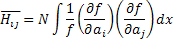
Для вычисления обратной матрицы H-1 имеется следующее правило:
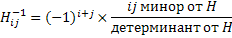 , так
, так 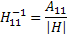 ,
где |H| - детерминант матрицы H, а А - алгебраическое дополнение.
,
где |H| - детерминант матрицы H, а А - алгебраическое дополнение.
Автокорреляционной функцией случайного процесса x(t) называется функция двух переменных t1 и t2, которая определяется равенством (под переменными t1 и t2 подразумеваются два момента времени, отстоящие друг от друга на определенную величину):
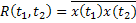
На практике для вычислений можно воспользоваться следующей формулой:
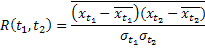
Previous: 10.31 Семантические сети
UP:
10 Приложения |