Previous: 10.29 10 правил Хольцмана и рекомендации для написания программ, критичных в отношении безопасности
UP:
10 Приложения |
Previous: 10.29 10 правил Хольцмана и рекомендации для написания программ, критичных в отношении безопасности
UP:
10 Приложения |
10.30 Базовые определения теории информации
Семенов Ю.А. (ГНЦ ИТЭФ)
Если мы проводим статистически испытания и возможно k равновероятных исходов, то степень неопределенности результата отдельного испытания определяется величиной k. При k=1 исход испытания не является случайным, а при большом k предсказыть исход испытания становится проблематичным.
Характеристика степени неопределенности результата испытания должна быть функцией k и при k=1 обращаться в нуль, так как неопределенность в этом случае отсутствует.
Предположим, что имеется два независимых испытания А и Б и пусть А имеет k равновероятных исходов, при испытании Б возможны l равновероятных исходов. Тогда комбинированное испытание АБ будет иметь неопределенность равную сумме неопределенностей испытания А и Б, ведь неопределенность испытания АБ характеризуется числом возможных исходов k×l. Этот факт наводит на мысль, что степень неопределенности испытания при k равновероятных исходах должна характеризоваться log(k).
Каждый отдельный исход, имеющий вероятность 1/k, вносит неопределенность, равную (1/k)×log(k).
Если в исходный момент времени степень неопределенности характеризовалась величиной Е1, а после реализации события А неопределенность стала равной Е2, причем Е1>Е2, то можно считать, что мы получили количество информации, равное Е1 - Е2, сопряженное с событием А. Для каналов передачи данных транспортировка ложного сообщения или информации о величайшем открытии, характерищующегося тем же числом бит, требует идентичных ресурсов. Мы привыкли мерить количество информации числом бит. Безусловно это не вполне корректно. Ведь можно передать из одной точки в другую терабайт нулей, при этом вряд ли можно говорить о большом объеме переданной информации.
Более корректной оценкой количества информации можно считать число байт в архивированном файле. Современные методы архивации приближаются к энтропийному пределу и это дает заведомо лучшую оценку, чем число байт в неархивированном файле.
В 1928 Ральфом Хартли была предложена формула для оценки количества информации в сообщении, содержащем n букв. Число букв в алфавите считается равным m. Количество возможных вариантов разных сообщений N для данного алфавита из m букв равно mn. Формула Хартли определяет число бит в сообщении длиной n I=log2N= n log2m.
Генный набор человека характеризуется примерно 2 Гбайт, людей на земле уже около 10 миллиардов. Таким образом, для описания генных наборов всех людей потребуется около 20 экзабайт данных. Но можно ли утверждать, что эти экзабайты информационно более емки, чем формула E=m×c2? То есть существенным является не только количество информации, но и ее практическая важность (область прагматики).
Проблема оценки качества информации всегда была актуальной. Я после онончания института много работал и времени для чтения было мало. По это причине я выбирал книги, написанные до 17-го века, так как они дошли до нас благодаря переписчикам. Я полагал, что плохую книгу не стали бы переписывать. Сегодня одним из критериев качества стал индекс цитирования. Его пытаются фальсифицировать с помощью алгоритма "кукушка хвалит петуха за то, что хвалит он кукушку". Но лучших критериев качества пока не придумано. Для программ одним из критериев качества можно считать число ошибок на 1000 строк кода.
Если число букв в алфавите равно n, а количество используемых элементарных сигналов - m, то при любом методе кодирования среднее число элементарных сигналов на одну букву алфавита не может быть меньше {log(n)/log(m)}. Однако оно может быть сколь угодно близко к этому отношению. В простейшем случае, когда при передаче используется только два уровня сигнала, m=2, т.е. число бит на одну букву равно log(n)/log(2).
Часто встречающиеся символы содержат малое количество информации, а редко встречающиеся большее. Если i-й символ определяется в результате ki альтернативных выборов, то вероятность его появления равна (1/2)ki. Соответственно для выбора символа, который встречается с вероятностью pi, нужно ki= log2(1/pi) выборов. Смотри раздел Статический алгоритм Хафмана.
Количество информации, содержащееся в символе, которое определяется частотой его появления, равно:
log2(1/pi) [бит]
Отсюда среднее количество информации на один произвольный символ равно:
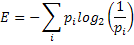
E называют средним количеством информации на символ или энтропией источника информации. Результатом отдельного альтернативного выбора может быть <0> или <1>. Тогда всякому символу соответствует некоторая последовательность <0> и <1>. Такая последовательность является кодировкой символа. Энтропия одной буквы русского языка равна примерно Е1≈4,35 бит.
Если при некотором кодировании символов i-ый символ имеет длину Ni, то средняя длина слов равна:
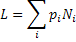
Если предположить, что набор символов можно поделить на равновероятные подмножества, то L=E. Следует иметь в виду, что на самом деле всегда E ≤ L (следствие теоремы кодирования Шеннона).
Разность L-E называется избыточностью кода, а 1-(E/L) - относительной избыточностью кода. Смотри раздел "Коррекция ошибок".
Так как на практике отдельные символы встречаются с разной вероятностью, то кодирование с постоянной длиной кодовых слов обычно является избыточным. Так все стандартные 8-битовые кодировки русского алфавита являются избыточными. Значение энтропии для русского языка ≤ 4,35. Для точной оценки энтропии следует учесть вероятности различных пар и троек символов. Такой учет из-за корреляционных зависимостей может понизить значение Е. Учет вероятности всевозможных групп символов может понизить Е почти до уровня ≈1 бит на символ.
Представленные выше логарифмические зависимости косвенно подтверждаются законом Меркеля (1885 г). Время реакции испытуемого при требовании выбора определенного предмета из N имеющихся пропорционально log(N).
| Пожалуй, интерес к сенсациям диктуется интуитивным стремлением людей получить информационно более емкий материал. Если бы мы научились корректно определять истинное количество информации в научной статье, то присуждение нобелевской премии превратилось бы в простую формальность. |
Если рассмотреть процесс подбрасывания монеты, то энтропия неизвестного результата следующего бросания максимальна, если вероятности выпадания каждой из сторон монеты равны (максимальная неопределенность; вероятностью вставания монеты на ребро пренебрегаем).
Обычный способ определения энтропии текста базируется на модели Маркова для текста. При этом вероятность появления очередного символа предполагается независимой от предыдущего символа (что, разумеется не всегда верно).
Если мы имеем n-буквенный алфавит и используем m-ичныйое кодовое представление (m уровней сигнала, при m=2 получем двоичное представление), то для передачи одной буквы может требоваться ~log(n)/log(m) элементарных сигналов.
Основная теорема кодирования. При кодировании сообщения, разбитого на N-буквенные блоки, можно, выбрав N достаточно большим, добиться того, чтобы среднее число двоичных элементарных сигналов, приходящихся на одну букву исходного сообщения, было сколь угодно близко к отношению количества информации, содержаейся в одной букве, к одному биту (Е).
В общем случае взаимозависимых букв значение энтропии Е одной буквы следует заменить удельной энтропией Е∞ = lim(E(N))/N) при N → ∞, где Е(N) - энтропия из N букв.
Разность R = 1 - E∞/H0 показывает, насколько меньше единицы отношение предельной энтропии E∞ к величине H0 = log(n), которая характеризует наибольшую информацию, содержащуюся в одной букве алфавита с данным числом букв. Шеннон назвал эту разность избыточностью языка. Избыточность русского языка превышает 50%.
Одной из заслуг Шеннона является установление факта зависимости ограничения пропускной способности канала от уровня шума.
Иногда энтропия выражается в битах в секунду. Если для канала без памяти энтропия символа равна Е, и если источник генерирует один символ каждые t секунд, то энтропия в битах в секунду равна E/t.
Если по линии связи в единицу времени можно передать L элементарных сигналов, принимающих m различных значений, то скорость передачи сообщений не может быть больше чем:
v = (L log(m))/E букв/ед. времени
Числитель этого выражения зависит лишь от канала связи, а знаминатель характеризует само сообщение.
Для каждого канала без памяти, емкость канала С=supI(X;Y) имеет следующее свойство (теорема Шеннона).
<Передатчик> → X → <Канал с шумом> → Y → <Приемник>
Для любого e> 0 и R<C, для достаточно большого N, существует код длиной N и скорость передачи ≥ R и алгоритм декодирования, при котором максимальная блочная ошибка ≤ e.
Если вероятность ошибки при передаче бита (BER) pb приемлема, то достижимы скорости передачи вплоть до R(pb), где
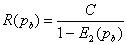
и E2(pb) является двоичной энтропийной функцией
E2(pb)= -[pb log pb + (1- pb) log(1-pb)]
Для любого pb, скорости передачи выше R(pb) не достижимы.
Для случая "белого" гауссова шума, когда все частоты имеют равные уровни, а амплитуды имеют гауссово распределение имеем:
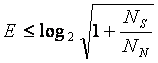
где NS - средняя мощность сигнала, а NN - средняя можность шума. Из этой формулы непосредственно следует традиционная формула теоремы Шеннона для канала с заданной полосой пропускания и уровнем шума.
Энтропия указывает предельный уровень сжатия данных архиваторами. Написать программу, которая бы обеспечила более высокий уровень сжатия теоретически невозможно. Величина сжатия определяется избыточностью обрабатываемого массива бит. Каждый из естественных языков обладает определенной избыточностью. Среди европейских языков русский обладает одной из самых высоких уровней избыточности. Об этом можно судить по размерам русского перевода английского текста. Обычно он примерно на 30% больше.
Пусть имеется два независимых опыта Х и У с таблицами вероятностей исходов:
| Исходы испытания | X1 | X2 | ... | Xk |
| Вероятности | p(X1) | p(X2) | ... | P(Xk) |
| Исходы испытания | Y1 | Y2 | ... | Ym |
| Вероятности | p(Y1) | p(Y2) | ... | P(Ym) |
Рассмотрим составной эксперимент , состоящий в том, что одновременно выполняются испытания Х и У. Такой эксперимент может иметь km исходов:
X1Y1,X1Y2,...,X1Ym; A2Y1, X2Y2,...,X2Ym;....; XkY1, XkY2,...,XkYm,
где X1Y1 означает, что эксперимент X имел исход X1, а эксперимент Y - исход Y1. Понятно, что неопределенность эксперимента XY будет больше неопределенности каждого из X и Y в отдельности. Энтропия T(XY=E(X) + E(Y).
Если теперь предположить, что результаты опытов X и Y не являются независимыми. В этом случае уже нельзя предполагать, что энтропия составного опыта XY может быть равна сумме энтропий X и Y. Энтропия составного опыта XY будет равна:
E(XY) = - p(X1Y1)log(p(X1Y1)) - p(X1Y2)log(p(X1Y2)) - ... - p(X1Ym)log(p(X1Ym)) - ...
- p(X2Y1)log(p(X2Y1)) - p(X2Y2)log(p(X2Y2)) - ... - p(X2Ym)log(p(X2Ym)) - ...
- p(XkY1)log(p(XkY1)) - p(XkY2)log(p(XkY2)) - ... - p(XkYm)log(p(XkYm)) ,
Здесь уже нельзя заменить вероятности p(X1Y1), p(X1Y2) и т.д. произведениями вероятностей (p(X1Y1) не равно p(X1)p(Y1), а p(X1)pX1(Y1) - условная вероятность события Y1 при условии X1. Энтропия ЕХ(У) называется условной энтропией опыта Y при условии реализации опыта X.
EX(Y) = p(X1)EX1(Y) + p(Y2)EX2(Y) + ... + p(Xk) EXk(Y) или
E(XY) = E(X) + EX(Y)
В любом случае
0 ≤ EX(Y) ≤ E(Y)
Условные значения энтропии для двухбуквенных и трехбуквенных комбинаций в русском языке равны:
E0=log(32)=5; E1=4,35; E2= 3,52; E3= 3,01
При языковых исследованиях следует учитывать то, что появление в тексте определенной буквы меняет распределение вероятностей для следующей. Так появление буквы "е" делает весьма вероятным появление еще одной буквы "e". Но появление комбинации "ee" делает появление еще одного "e" крайне мало вероятным. Примеров таких корреляций можно привести достаточно много.
Для языков, использующих латинский алфавит, частоты использования отдельных букв весьма различны. Так если разместить символы букв по мере убывания их частоты использования, то для английского языка мы получим _ETAONRI..., для немецкого - _ENISTRAD... и для французского - _ESANITUR... .Во всех случаях символ _ обозначает пробел между словами.
Классическое определение информационной энтропии (H) выглядит как:
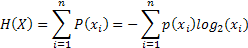
где pi - вероятность того, что реализуется конкретное значение хi (i может принимать значения от 1 до n. I(x) - целочисленная случайная функция (информационное содержимое Х).
Previous: 10.29 10 правил Хольцмана и рекомендации для написания программ, критичных в отношении безопасности
UP:
10 Приложения |