Previous: 2.7 Обнаружение ошибок
UP:
2 Преобразование, кодировка и передача информации |
Previous: 2.7 Обнаружение ошибок
UP:
2 Преобразование, кодировка и передача информации |
2.8 Коррекция ошибок
Семенов Ю.А. (ГНЦ ИТЭФ)

Исправлять ошибки труднее, чем их детектировать или предотвращать. Процедура коррекции ошибок предполагает два совмещенные процесса: обнаружение ошибки и определение места (идентификация сообщения и позиции в сообщении). После решения этих двух задач, исправление тривиально - надо инвертировать значение ошибочного бита. В наземных каналах связи, где вероятность ошибки невелика, обычно используется метод детектирования ошибок и повторной пересылки фрагмента, содержащего дефект. Для спутниковых каналов с типичными для них большими задержками системы коррекции ошибок становятся привлекательными. Здесь используют коды Хэмминга или коды свертки.
Но существуют и более простые методы коррекции ошибок. Например, передача блока данных, содержащего N строк и M столбцов, снабженных битами четности для каждой строки и столбца. Обнаружение ошибки четности в строке i и столбце j указывает на бит, который должен быть инвертирован. Может показаться, что в случае, когда неверны два бита, находящиеся в разных строках и столбцах, они также могут быть исправлены. Но это не так. Ведь нельзя разделить варианты i1,j1 - i2,j2 и i1,j2 - i2,j1.
Этот метод может быть развит путем формирования блока данных с N строками, M столбцами и K слоями. Здесь биты четности формируются для всех строк и столбцов каждого из слоев, а также битов, имеющих одинаковые номера строк и столбцов i,j. Полное число битов четности в этом случае равно (N+M+1)×K +(N+1)×(M+1). Если M=N=K=8, число бит данных составит 512, а число бит четности - 217. Нетрудно видеть, что в этом случае число исправляемых ошибок будет больше 1. Смотри рис. 1.
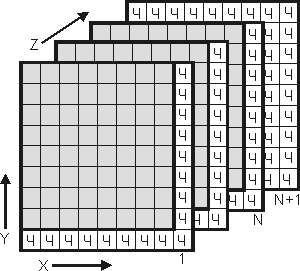
Рис. 1. Метод коррекции более одной ошибки в блоке данных (битам данных соответствуют окрашенные квадраты)
Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Обычно код Хэмминга характеризуется двумя целыми числами, например, (11,7) используемый при передаче 7-битных ASCII-кодов. Такая запись говорит, что при передаче 7-битного кода используется 4 контрольных бита (7+4=11). При этом предполагается, что имела место ошибка в одном бите и что ошибка в двух или более битах существенно менее вероятна. С учетом этого исправление ошибки осуществляется с определенной вероятностью. Например, пусть возможны следующие правильные коды (все они, кроме первого и последнего, отстоят друг от друга на расстояние 4):
00000000
11110000
00001111
11111111
При получении кода 00000111 не трудно предположить, что правильное значение полученного кода равно 00001111. Другие коды отстоят от полученного на большее расстояние Хэмминга. Расстояние Хэмминга для двух кодов равной длины равно числу разных бит в этих кодах.
Рассмотрим пример передачи кода буквы s = 0x073 = 1110011 с использованием кода Хэмминга (11,7).
| Позиция бита: | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Значение бита: | 1 | 1 | 1 | * | 0 | 0 | 1 | * | 1 | * | * |
Символами * помечены четыре позиции, где должны размещаться контрольные биты. Эти позиции определяются целой степенью 2 (1, 2, 4, 8 и т.д.). Контрольная сумма формируется путем выполнения операции XOR (исключающее ИЛИ) над кодами позиций ненулевых битов. В данном случае это 11, 10, 9, 5 и 3. Вычислим контрольную сумму:
| 11 = | 1011 |
| 10 = | 1010 |
| 09 = | 1001 |
| 05 = | 0101 |
| 03 = | 0011 |
| S = | 1110 |
Таким образом, приемник получит код:
| Позиция бита: | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Значение бита: | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Просуммируем снова коды позиций ненулевых битов и получим нуль.
| 11 = | 1011 |
| 10 = | 1010 |
| 09 = | 1001 |
| 08 = | 1000 |
| 05 = | 0101 |
| 04 = | 0100 |
| 03 = | 0011 |
| 02 = | 0010 |
| S = | 0000 |
Ну а теперь рассмотрим два случая ошибок в одном из битов посылки, например, в бите 7 (1 вместо 0) и в бите 5 (0 вместо 1). Просуммируем коды позиций ненулевых бит еще раз.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
В обоих случаях контрольная сумма равна позиции бита, переданного с ошибкой. Теперь для исправления ошибки достаточно инвертировать бит, номер которого указан в контрольной сумме. Понятно, что если ошибка произойдет при передаче более чем одного бита, код Хэмминга при данной избыточности окажется бесполезен.
В общем случае код имеет N=M+C бит и предполагается, что не более чем один бит в коде может иметь ошибку. Тогда возможно N+1 состояние кода (правильное состояние и n ошибочных). Пусть М=4, а N=7, тогда слово-сообщение будет иметь вид: M4, M3, M2, C3, M1, C2, C1. Теперь попытаемся вычислить значения С1, С2, С3. Для этого используются уравнения, где все операции представляют собой сложение по модулю 2:
С1 = М1 + М2 + М4
С2 = М1 + М3 + М4
С3 = М2 + М3 + М4
Для определения того, доставлено ли сообщение без ошибок, вычисляем следующие выражения (сложение по модулю 2):
С11 = С1 + М4 + М2 + М1
С12 = С2 + М4 + М3 + М1
С13 = С3 + М4 + М3 + М2
Результат вычисления интерпретируется следующим образом.
| С11 | С12 | С13 | Значение |
| 1 | 2 | 4 | Позиция бит |
| 0 | 0 | 0 | Ошибок нет | 0 | 0 | 1 | Бит С3 не верен |
| 0 | 1 | 0 | Бит С2 не верен |
| 0 | 1 | 1 | Бит М3 не верен |
| 1 | 0 | 0 | Бит С1 не верен |
| 1 | 0 | 1 | Бит М2 не верен |
| 1 | 1 | 0 | Бит М1 не верен |
| 1 | 1 | 1 | Бит М4 не верен |
Описанная схема легко переносится на любое число n и М.
Число возможных кодовых комбинаций М помехоустойчивого кода делится на n классов, где N - число разрешенных кодов. Разделение на классы осуществляется так, чтобы в каждый класс вошел один разрешенный код и ближайшие к нему (по расстоянию Хэмминга) запрещенные коды. В процессе приема данных определяется, к какому классу принадлежит пришедший код. Если код принят с ошибкой, он заменяется ближайшим разрешенным кодом. При этом предполагается, что кратность ошибки не более qm.
Можно доказать, что для исправления ошибок с кратностью не более qm кодовое расстояние должно превышать 2qm (как правило, оно выбирается равным D = 2qm +1). В теории кодирования существуют следующие оценки максимального числа N n-разрядных кодов с расстоянием D.
| d=1 | n=2n |
| d=2 | n=2n-1 |
| d=3 | n 2n /(1+n) |
| d=2q+1 | 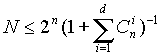 (для кода Хэмминга это неравенство превращается в равенство) (для кода Хэмминга это неравенство превращается в равенство) |
В случае кода Хэмминга первые k разрядов используются в качестве информационных, причем
k= n - log(n+1),
откуда следует (логарифм по основанию 2), что k может принимать значения 0, 1, 4, 11, 26, 57 и т.д., это и определяет соответствующие коды Хэмминга (3,1); (7,4); (15,11); (31,26); (63,57) и т.д.
Обобщением кодов Хэмминга являются циклические коды BCH (Bose-Chadhuri-Hocquenghem). Это коды с широким выбором длины и возможностей исправления ошибок. Циклические коды характеризуются полиномом g(x) степени n-k, g(x) = 1 + g1x + g2x2 + … + xn-k. g(x) называется порождающим многочленом циклического кода. Если многочлен g(x) n-k и является делителем многочлена xn + 1, то код C(g(x)) является линейным циклическим (n,k)-кодом. Число циклических n-разрядных кодов равно числу делителей многочлена xn + 1.
При кодировании слова все кодовые слова кратны g(x). g(x) определяется на основе сомножителей полинома xn +1 как:
xn +1 = g(x)h(x)
Например, если n=7 (x7+1), его сомножители (1 + x + x3)(1 + x + x2 + x4), а g(x) = 1+x + x3.
Чтобы представить сообщение h(x) в виде циклического кода, в котором можно указать постоянные места проверочных и информационных символов, нужно разделить многочлен xn-kh(x) на g(x) и прибавить остаток от деления к многочлену xn-kh(x). См. Л.Ф. Куликовский и В.В. Мотов, “Теоретические основы информационных процессов”. Москва “Высшая школа” 1987. Привлекательность циклических кодов заключается в простоте аппаратной реализации с использованием сдвиговых регистров.
Пусть общее число бит в блоке равно N, из них полезную информацию несут в себе K бит, тогда в случае ошибки, имеется возможность исправить m бит. Таблица 2.8.1 содержит зависимость m от N и K для кодов ВСН.
Таблица 2.8.1
| Общее число бит N | Число полезных бит М | Число исправляемых бит m |
| 31 | 26 | 1 |
| 21 | 2 | |
| 16 | 3 | |
| 63 | 57 | 1 |
| 51 | 2 | |
| 45 | 3 | |
| 127 | 120 | 1 |
| 113 | 2 | |
| 106 | 3 |
Увеличивая разность N-M, можно не только нарастить число исправляемых бит m, но открыть возможность обнаружить множественные ошибки. В таблице 2.8.2 приведен процент обнаруживаемых множественных ошибок в зависимости от M и N-M.
Таблица 2.8.2
| Число полезных бит М | Число избыточных бит (n-m) | ||
| 6 | 7 | 8 | |
| 32 | 48% | 74% | 89% |
| 40 | 36% | 68% | 84% |
| 48 | 23% | 62% | 81% |
Другой блочный метод предполагает “продольное и поперечное” контрольное суммирование предаваемого блока. Блок при этом представляется в виде N строк и M столбцов. Вычисляется биты четности для всех строк и всех столбцов, в результате получается два кода, соответственно длиной N и M бит. На принимающей стороне биты четности для строк и столбцов вычисляются повторно и сравниваются с присланными. При выявлении отличия в бите i кода битов четности строк и бите j - кода столбцов, позиция неверного бита оказывается определенной (i,j). Понятно, что если выявится два и более неверных битов в контрольных кодах строк и столбцов, задача коррекции становится неразрешимой. Уязвим этот метод и для двойных ошибок, когда сбой был, а контрольные коды остались корректными.
Применение кодов свертки позволяют уменьшить вероятность ошибок при обмене, даже если число ошибок при передаче блока данных больше 1.
Блочный код определяется, как набор возможных кодов, который получается из последовательности бит, составляющих сообщение. Например, если мы имеем К бит, то имеется 2К возможных сообщений и такое же число кодов, которые могут быть получены из этих сообщений. Набор этих кодов представляет собой блочный код. Линейные коды получаются в результате перемножения сообщения М на порождающую матрицу G[IA]. Каждой порождающей матрице ставится в соответствие матрица проверки четности (n-k)*n. Эта матрица позволяет исправлять ошибки в полученных сообщениях путем вычисления синдрома. Матрица проверки четности находится из матрицы идентичности i и транспонированной матрицы А. G[IA] ==> H[ATI].
| I | A | AT |
Если 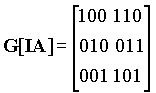 , то H[ATI] =
, то H[ATI] = 
Синдром полученного сообщения равен
S = [полученное сообщение]. [матрица проверки четности].
Если синдром содержит нули, ошибок нет, в противном случае сообщение доставлено с ошибкой. Если сообщение М соответствует М=2k, а k =3 высота матрицы, то можно записать восемь кодов:
| Сообщения | Кодовые вектора | Вычисленные как |
| M1 = 000 | V1 = 000000 | M1.G |
| M2 = 001 | V2 = 001101 | M2.G |
| M3 = 010 | V3 = 010011 | M3. G |
| M4 = 100 | V4 = 100110 | M4. G |
| M5 = 011 | V5 = 011110 | M5.G |
| M6 = 101 | V6 = 101011 | M6 .G |
| M7 = 110 | V7 = 110101 | M7 .G |
| M8 = 111 | V8 = 111000 | M8 .G |
Кодовые векторы для этих сообщений приведены во второй колонке. На основе этой информации генерируется таблица 2.8.3, которая называется стандартным массивом. Стандартный массив использует кодовые слова и добавляет к ним биты ошибок, чтобы получить неверные кодовые слова.
Таблица 2.8.3. Стандартный массив для кодов (6,3)
| 000000 | 001101 | 010011 | 100110 | 011110 | 101011 | 110101 | 111000 |
| 000001 | 001100 | 010010 | 100111 | 011111 | 101010 | 110100 | 111001 |
| 000010 | 001111 | 010001 | 100100 | 011100 | 101001 | 110111 | 111010 |
| 000100 | 001001 | 010111 | 100010 | 011010 | 101111 | 110001 | 111100 |
| 001000 | 000101 | 011011 | 101110 | 010110 | 100011 | 111101 | 110000 |
| 010000 | 011101 | 000011 | 110110 | 001110 | 111011 | 100101 | 101000 |
| 100000 | 101101 | 110011 | 000110 | 111110 | 001011 | 010101 | 011000 |
| 001001 | 000100 | 011010 | 101111 | 010111 | 100010 | 111100 | 011001 |
Предположим, что верхняя строка таблицы содержит истинные значения переданных кодов. Из таблицы 2.8.3 видно, что, если ошибки случаются в позициях, соответствующих битам кодов из левой колонки, можно определить истинное значение полученного кода. Для этого достаточно полученный код сложить с кодом в левой колонке посредством операции XOR.
Синдром равен произведению левой колонки (CL "coset leader") стандартного массива на транспонированную матрицу контроля четности HT.
| Синдром = CL . HT | Левая колонка стандартного массива |
| 000 | 000000 |
| 001 | 000001 |
| 010 | 000010 |
| 100 | 000100 |
| 110 | 001000 |
| 101 | 010000 |
| 011 | 100000 |
| 111 | 001001 |
Чтобы преобразовать полученный код в правильный, нужно умножить полученный код на транспонированную матрицу проверки четности, с тем чтобы получить синдром. Полученное значение левой колонки стандартного массива добавляется (XOR!) к полученному коду, чтобы получить его истинное значение. Например, если мы получили 001100, умножаем этот код на HT:
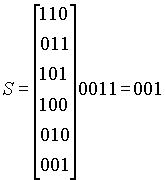
этот результат указывает на место ошибки, истинное значение кода получается в результате операции XOR:
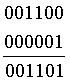 под горизонтальной чертой записано истинное значение кода.
под горизонтальной чертой записано истинное значение кода.
Транспортировка данных подвержена влиянию шумов и наводок, которые вносят искажения. Если вероятность повреждения данных мала, достаточно зарегистрировать сам факт искажения и повторить передачу поврежденного фрагмента.
Когда вероятность искажения велика, например, в каналах коммуникаций с геостационарными спутниками, используются методы коррекции ошибок. Одним из таких методов является FEC (Forward Error Correction, иногда называемое канальным кодированием [1]). Технология FEC последнее время достаточно широко используется в беспроводных, локальных сетях (WLAN). Существуют две основные разновидности FEC: блочное кодирование и кодирование по методу свертки.
Блочное кодирование работает с блоками (пакетами) бит или символов фиксированного размера. Метод свертки работает с потоками бит или символов произвольной протяженности. Коды свертки при желании могут быть преобразованы в блочные коды.
Существует большое число блочных кодов, одним из наиболее важных является алгоритм Рида-Соломона, который используется при работе с CD, DVD и жесткими дисками ЭВМ. Блочные коды и коды свертки могут использоваться и совместно.
Для FEC-кодирования иногда используется метод свертки, который впервые был применен в 1955 году. Главной особенностью этого метода является сильная зависимость кодирования от предыдущих информационных битов и высокие требования к объему памяти. FEC-код обычно просматривает при декодировании 2-8 бит десятки или даже сотни бит, полученных ранее. Смотри также RFC-3452, -3453, -3695, -5052.
В 1967 году Эндрю Витерби (Andrew Viterbi) разработал технику декодирования, которая стала стандартной для кодов свертки. Эта методика требовала меньше памяти. Метод свертки более эффективен, когда ошибки распределены случайным образом, а не группируются в кластеры. Работа же с кластерами ошибок более эффективна при использовании алгебраического кодирования.
Одним из широко используемых разновидностей коррекции ошибок является турбо кодирование, разработанное американской аэрокосмической корпорацией. В этой схеме комбинируется два или более относительно простых кодов свертки. В FEC, также как и в других методах коррекции ошибок (коды Хэмминга, алгоритм Рида-Соломона и др.), блоки данных из k бит снабжаются кодами четности, которые пересылаются вместе с данными, и обеспечивают не только детектирование, но и исправление ошибок. Каждый дополнительный (избыточный) бит является сложной функцией многих исходных информационных бит. Исходная информация может содержаться в выходном передаваемом коде, тогда такой код называется систематическим, а может и не содержаться.
В результате через канал передается n-битовое кодовое слово (n>k). Конкретная реализация алгоритма FEC характеризуется комбинацией (n,k). Применение FEC в Интернет регламентируется документом RFC-3452. Коды FEC могут исключить необходимость обратной связи при потере или искажении доставленных данных (запросы повторной передачи). Особенно привлекательна технология FEC при работе с мультикастинг-потоками, где ретрансмиссия не предусматривается (см. RFC-3453).
В 1974 году Йозеф Оденвальдер (Joseph Odenwalder) объединил возможности алгебраического кодирования и метода свертки. Хорошего результата можно добиться, введя специальную операцию псевдослучайного перемешивания бит (interleaver).
В 1993 году группой Клода Берроу (Claude Berrou) был разработан турбо код. В кодеке, реализующем этот алгоритм, содержатся кодировщики как минимум двух компонент (реализующие алгебраический метод или свертку). Кодирование осуществляется для блоков данных. Здесь также используется псевдослучайное перемешивание бит перед передачей. Это приводит к тому, что кластеры ошибок, внесенных при транспортировке, оказываются разнесенными случайным образом в пределах блока данных.
На рис. 2. проводится сравнение вариантов BER (bit error rate) при обычной транспортировке данных через канал и при передаче тех же данных с использованием коррекции ошибок FEC для разных значений отношения сигнал-шум (S/N). Из этих данных видно, что при отношении S/N= 8 дБ применение FEC позволяет понизить BER примерно в 100 раз. При этом достигается результат, близкий (в пределах одного децибела) к теоретическому пределу Шеннона.
За последние пять лет были разработаны программы, которые позволяют оптимизировать структуры турбо-кодов. Улучшение BER для турбо-кодов имеет асимптотический предел и дальнейшее увеличение S/N уже не дает никакого выигрыша. Но схемы, позволяющие смягчить влияние этого насыщения, продолжают разрабатываться.
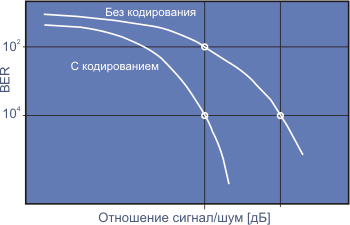
Рис. 2.
Турбо кодек должен иметь столько же компонентных декодеров, сколько имеется кодировщиков на стороне передатчика. Декодеры соединяются последовательно
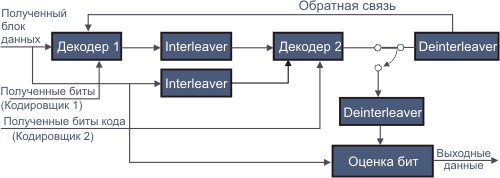
Рис. 3. Турбо декодер
Техника FEC находит все большее применение в телекоммуникациях, например, при передачи мультимедиа [2].
| Следует помнить, что как в случае FEC, так и в других известных методах коррекции ошибок, (BCH, Golay, Hamming и др.) скорректированный код является верным лишь с определенной конечной вероятностью. |
| 1 | http://www.aero.org/publication/crosslink/winter2002/04.html. Crosslink - The Aerospace Corporation magazine of advances in aerospace technology. The Aerospace Corporation (Volume 3, Number 1 (Winter 2001/2002)). |
| 2 | Multiple Description Source Coding using Forward Error Correction Codes, Rohit Puri, Kannan Ramchandran, University of California, Berkeley (rpuri, kannan@eecs.berkeley.edu). |
| 3 | http://en.wikipedia.org/wiki/Forward_error_correction |
| 4 | http://www.eccpage.com/, Morelos-Zaragoza, Robert (2004). The Error Correcting Codes (ECC) Page |
Коды Рида-Соломона были предложены в 1960 Ирвином Ридом (Irving S. Reed) и Густавом Соломоном (Gustave Solomon), являвшимися сотрудниками Линкольнской лаборатории МТИ. Ключом к использованию этой технологии стало изобретение эффективного алгоритма декодирования Элвином Беликамфом (Elwyn Berlekamp; http://en.wikipedia.org/wiki/Berlekamp-Massey_algorithm), профессором Калифорнийского университета (Беркли). Коды Рида-Соломона (см. также http://www.4i2i.com/reed_solomon_codes.htm) базируются на блочном принципе коррекции ошибок и используются в огромном числе приложений в сфере цифровых телекоммуникаций и при построении запоминающих устройств. Коды Рида-Соломона применяются для исправления ошибок во многих системах, включая:
На рис. 4 показаны практические приложения (дальние космические проекты) коррекции ошибок с использованием различных алгоритмов (Хэмминга, кодов свертки, Рида-Соломона и пр.). Данные и сам рисунок взяты из http://en.wikipedia.org/wiki/Reed-Solomon_error_correction..
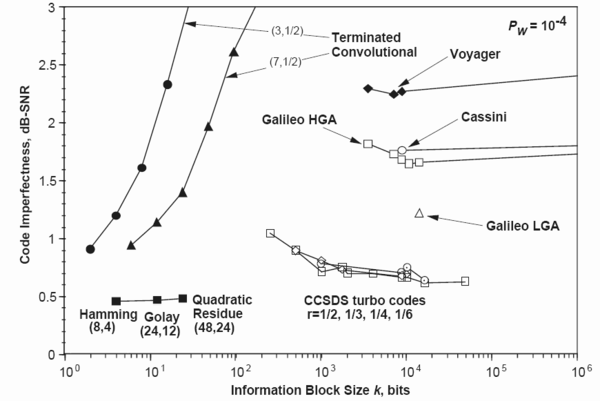
Рис. 4. Несовершенство кода, как функция размера информационного блока для разных задач и алгоритмов
Типовая система представлена ниже (см. http://www.4i2i.com/reed_solomon_codes.htm):

Рис. 5. Схема коррекции ошибок Рида-Соломона
Кодировщик Рида-Соломона берет блок цифровых данных и добавляет дополнительные "избыточные" биты. Ошибки происходят при передаче по каналам связи или по разным причинам при запоминании (например, из-за шума или наводок, царапин на CD и т.д.). Декодер Рида-Соломона обрабатывает каждый блок, пытается исправить ошибки и восстановить исходные данные. Число и типы ошибок, которые могут быть исправлены, зависят от характеристик кода Рида-Соломона.
Коды Рида-Соломона являются субнабором кодов BCH и представляют собой линейные блочные коды. Код Рида-Соломона специфицируются как RS(n,k) s-битных символов..
Это означает, что кодировщик воспринимает k информационных символов по s бит каждый и добавляет символы четности для формирования n символьного кодового слова. Имеется n-k символов четности по s бит каждый. Декодер Рида-Соломона может корректировать до t символов, которые содержат ошибки в кодовом слове, где 2t = n-k.
Диаграмма, представленная ниже, показывает типовое кодовое слово Рида-Соломона:

Рис. 6. Структура кодового слова R-S
Пример: Популярным кодом Рида-Соломона является RS(255,223) с 8-битными символами. Каждое кодовое слово содержит 255 байт, из которых 223 являются информационными и 32 байтами четности. Для этого кода:
n = 255, k = 223, s = 8
2t = 32, t = 16
Декодер может исправить любые 16 символов с ошибками в кодовом слове: то есть, ошибки могут быть исправлены, если число искаженных байт не превышает 16.
При размере символа s, максимальная длина кодового слова (n) для кода Рида-Соломона равна n = 2s – 1.
Например, максимальная длина кода с 8-битными символами (s=8) равна 255 байтам.
Коды Рида-Соломона могут быть в принципе укорочены путем обнуления некоторого числа информационных символов на входе кодировщика (передавать их в этом случае не нужно). При передаче данных декодеру эти нули снова вводятся в массив.
Пример: Код (255,223), описанный выше, может быть укорочен до (200,168). Кодировщик будет работать с блоком данных 168 байт, добавит 55 нулевых байт, сформирует кодовое слово (255,223) и передаст только 168 информационных байт и 32 байта четности.
Объем вычислительной мощности, необходимой для кодирования и декодирования кодов Рида-Соломона зависит от числа символов четности. Большое значение t означает, что большее число ошибок может быть исправлено, но это потребует большей вычислительной мощности по сравнению с вариантом при меньшем t.
Одна ошибка в символе происходит, когда 1 бит символа оказывается неверным или когда все биты не верны.
Пример: Код RS(255,223) может исправить до 16 ошибок в символах. В худшем случае, могут иметь место 16 битовых ошибок в разных символах (байтах). В лучшем случае, корректируются 16 полностью неверных байт, при этом исправляется 16 x 8=128 битовых ошибок.
Коды Рида-Соломона особенно хорошо подходят для корректировки кластеров ошибок (когда неверными оказываются большие группы бит кодового слова, следующие подряд).
Алгебраические процедуры декодирования Рида-Соломона могут исправлять ошибки и потери. Потерей считается случай, когда положение неверного символа известно. Декодер может исправить до t ошибок или до 2t потерь. Данные о потере (стирании) могут быть получены от демодулятора цифровой коммуникационной системы, т.е. демодулятор помечает полученные символы, которые вероятно содержат ошибки.
Когда кодовое слово декодируется, возможны три варианта:
В противном случае
или
Вероятность каждого из этих вариантов зависит от типа используемого кода Рида-Соломона, а также от числа и распределения ошибок.
Преимущество использования кодов Рида-Соломона заключается в том, что вероятность сохранения ошибок в декодированных данных обычно много меньше, чем вероятность ошибок, если коды Рида-Соломона не используются. Это часто называется выигрышем кодирования.
Пример: Пусть имеется цифровая телекоммуникационная системы, работающая с BER (Bit Error Ratio) равной 10-9, т.е. не более 1 из 109 бит передается с ошибкой. Такого результата можно достичь путем увеличения мощности передатчика или применением кодов Рида-Соломона (или другого типа коррекции ошибок). Алгоритм Рида-Соломона позволяет системе достичь требуемого уровня BER с более низкой выходной мощностью передатчика.
Кодирование и декодирование Рида-Соломона может быть выполнено аппаратно или программно.
Коды Рида-Соломона базируются на специальном разделе математики – полях Галуа (GF) или конечных полях. Арифметические действия (+, -, x, / и т.д.) над элементами конечного поля дают результат, который также является элементом этого поля. Кодировщик или декодер Рида-Соломона должны уметь выполнять эти арифметические операции. Эти операции для своей реализации требуют специального оборудования или специализированного программного обеспечения.
Кодовое слово Рида-Соломона формируется с привлечением специального полинома. Все корректные кодовые слова должны делиться без остатка на эти образующие полиномы. Общая форма образующего полинома имеет вид:
g(x) = (x-ai)(x-ai+1)…(x-ai+2t)
а кодовое слово формируется с помощью операции:
c(x) = g(x).i(x)
где g(x) является образующим полиномом, i(x) представляет собой информационный блок, c(x) – кодовое слово, называемое простым элементом поля.
Пример: Генератор для RS(255,249)
g(x)= (x-a0)(x-a1)(x-a2)(x-a3)(x-a4)(x-a5)
g(x)= x6 + g5x5 + g3x3 + g2x2 + g1x1 + g0
2t символов четности в кодовом слове Рида-Соломона определяются из следующего соотношения:.
p(x) = i(x)·x n-k mod g(x)
Ниже показана схема реализации кодировщика для версии RS(255,249):

Рис. 7. Схема кодировщика R-S
Каждый из 6 регистров содержит в себе символ (8 бит). Арифметические операторы выполняют сложение или умножение на символ как на элемент конечного поля..
Общая схема декодирования кодов Рида-Соломона показана ниже на рис. 8.
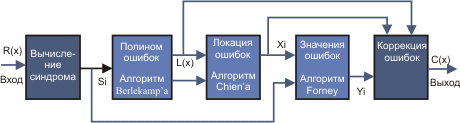
Рис. 8. Схема работы с кодами Рида-Соломона
Обозначения
r(x) Полученное кодовое слово
Si - Синдромы
L(x) - Полином локации ошибок
Xi - Положения ошибок
Yi - Значения ошибок
c(x) - Восстановленное кодовое слово
v - Число ошибок.
Полученное кодовое слово r(x) представляет собой исходное (переданное) кодовое слово c(x) плюс ошибки:.
r(x) = c(x) + e(x)
Декодер Рида-Соломона пытается определить позицию и значение ошибки для числа t ошибок (или 2t потерь) и исправить ошибки и потери.
Вычисление синдрома похоже на вычисление четности. Кодовое слово Рида-Соломона имеет 2t синдромов, это зависит только от ошибок (а не передаваемых кодовых слов). Синдромы могут быть вычислены путем подстановки 2t корней образующего полинома g(x) в r(x).
Это делается путем решения системы уравнений с t неизвестными. Существует несколько быстрых алгоритмов для решения этой задачи. Эти алгоритмы используют особенности структуры матрицы кодов Рида-Соломона и сильно сокращают необходимую вычислительную мощность. Делается это в два этапа:
Это может быть сделано с помощью алгоритма Berlekamp-Massey или алгоритма Эвклида. Алгоритм Эвклида используется чаще на практике, так как его легче реализовать, однако, алгоритм Berlekamp-Massey позволяет получить более эффективную реализацию оборудования и программ..
Здесь также нужно решить систему уравнений с t неизвестными. Для решения используется быстрый алгоритм Forney.
Существует несколько коммерческих аппаратных реализаций. Имеется много разработанных интегральных схем, предназначенных для кодирования и декодирований кодов Рида-Соломона. Эти ИС допускают определенный уровень программирования (например, RS(255,k), где t может принимать значения от 1 до 16).
До недавнего времени, программные реализации в "реальном времени" требовали слишком большой вычислительной мощности для практически всех кодов Рида-Соломона. Главной трудностью в программной реализации кодов Рида-Соломона являлось то, что процессоры общего назначения не поддерживают арифметические операции для поля Галуа. Однако оптимальное составление программ в сочетании с возросшей вычислительной мощностью позволяют получить вполне приемлемые результаты для относительно высоких скоростей передачи данных.
На рис. 9 показана фотография поверхности Марса, полученная американской станцией "Curiosity" (2012г). Сам Марс с Земли даже с помощью бинокля виден плохо. Современные методы коррекции ошибок позволяют получить приемелемы результат даже в условиях, когда шум на порядки превышает сигнал. Смотри также рис. 4.

Рис. 9. Фотография, полученная марсианской станцией Curiosity (США)
| [1] | Wicker, "Error Control Systems for Digital Communication and Storage", Prentice-Hall 1995 |
| [2] | Lin and Costello, "Error Control Coding: Fundamentals and Applications", Prentice-Hall 1983. |
| [3] | Clark and Cain, "Error Correction Coding for Digital Communications", Plenum 1988 |
| [4] | Wilson, "Digital Modulation and Coding", Prentice-Hall 1996 |
| [5] | http://en.wikipedia.org/wiki/Reed-Solomon_error_correction |
| [6] | http://en.wikipedia.org/wiki/Forward_error_correction (forward error correction) |
| [7] | http://en.wikipedia.org/wiki/BCH_code |
| [8] | http://www.cs.cornell.edu/Courses/cs722/2000sp/ReedSolomon.pdf. |
| [9] | http://www.ka9q.net/code/fec/ (Фил Карн) |
| [10] | http://www.radionetworkprocessor.com/reed-solomon.html (собрание ссылок на книги, статьи и программные коды) |
| [11] | http://rscode.sourceforge.net/ (библиотека программ) |
| [12] | http://www.artech-house.com/ (приложения для видео-коммуникаций) |
| [13] | http://www.cs.utk.edu/~plank/plank/papers/SPE-9-97.html (учебные материалы)d> |
| [14] | http://www.trl.ibm.co.jp/news/lead_rs_e.htm |
| [15] | http://www.sxlist.com/techref/method/error/rs-gp-pk-uoh-199609/index |
| [16] | http://www.csdmag.com/main/1999/06/9906building.htm |
| [17] | http://www.4i2i.com/products.htm (аппаратные и программные реализации) |
Смотри также www.cs.ucl.ac.uk/staff/S.Bhatti/D51-notes/node33.html (Saleem Bhatti).
Previous: 2.7 Обнаружение ошибок
UP:
2 Преобразование, кодировка и передача информации |