


 |
|
Previous: 6.4.10 Протокол аутентификации Нидхэма-Шредера в случаях симметричной и асимметричной системы шифрования
UP:
6.4 Системы шифрования |



 |
|
Previous: 6.4.10 Протокол аутентификации Нидхэма-Шредера в случаях симметричной и асимметричной системы шифрования
UP:
6.4 Системы шифрования |
Стандарт AES (Advanced Encryption Standard) является стандартом шифрования США, принятым в 2000-ом году. Он специфицирует алгоритм Rijndael http://www.nist.gov/CryptoToolkit (смотри также http://csrc.nist.gov/ publications/fips/fips197/fips-197.pdf). Этот алгоритм представляет собой симметричный блочный шифр, который работает с блоками данных длиной 128 бит и использует ключи длиной 128, 192 и 256 бит (версии AES-28; AES-192 и AES-256). Сам алгоритм может работать и с другими длинами блоков данных и ключей, но эта возможность в стандарт не вошла. При использовании 128-битного ключа для взлома шифрования по заявлению правительства США потребуется 149 триллионов лет.
Биты данных нумеруются с нуля, начиная со старших. В AES основным является полиномиальное представлением кодов. Так байт {01100011} следует представлять как: x6 +x5 + x + 1.
Алгоритм AES производит операции над двумерными массивами байт, называемыми структурами (state). Структура состоит из 4 рядов по Nb байт. Nb равно длине блока, деленной на 32 (в данном стандарте Nb=4). Это позволяет обозначать структуру как sr,c или s[r,c], где 0≤r<4 и 0≤с<4..
Входной код (in), который является последовательностью 16 байт можно представить как:
s[r,c] =in[r +4c]
При реализации алгоритма AES используются операции сложения байт (по модулю 2 = XOR) и умножения. В алгоритме AES при умножении байтов используется неприводимый многочлен:
| m(x) = x8 + x4 + x3 + x + 1 | [1] |
Вычисление произведения М байтов {b1} на {b2} здесь выполняется согласно следующему алгоритму:
| M=[{b1}●{b2}] mod m(x). | [2] |
В этом случае обратная величина байта равна:
| {b}-1 ={b} mod m(x) | [3] |
для умножения полубайтов (коды длиной 4 бита) используется неприводимый полином:
m2(x) = x4 + 1
Вычисление произведения М полубайтов {a} на {b} здесь выполняется следующим образом:
| M=[{a}●{b}] mod m2(x). | [2a] |
M представляет собой полубайт d. Операцию умножения полубайтов {a} на {b} можно записать в матричном виде:
 | [4] |
Как было сказано выше длины ключей Nk (длина, измеренная в 32 битных словах) могут принимать значения 4, 6 или 8 (для AES-128, -192 и -256, соответственно). Число итераций Nr (round), реализуемых в алгоритме AES, составляет соответственно 10, 12 и 14.
При запуске алгоритма шифрования входной блок данных копируется в массив state. После первоначального добавления к state ключа массив state преобразуется с помощью функции циклической обработки Nr раз (последний цикл несколько отличается от предыдущих, см. рис. 19.3). Результат преобразования заносится в выходной массив.
Описание алгоритма в С-подобном представлении отображено на рис. 1. Преобразования SubByte(), ShiftRows(), MixColumns() и AddRoundKey() осуществляют обработку массива state. Массив w[i] описан ниже.
| Cipher(byte in[4*Nb], byte out[4*Nb], word w[Nb*(Nr+1)]) begin byte state[4,Nb] state = in AddRoundKey(state, w[0, Nb-1]) for round = 1 step 1 to Nr–1 SubBytes(state) ShiftRows(state) MixColumns(state) AddRoundKey(state, w[round*Nb, (round+1)*Nb-1]) end for SubBytes(state) ShiftRows(state) AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1]) out = state end |
Рис. 1. Псевдокод, реализующий процедуру шифрования
Преобразование SubByte() является нелинейной подстановкой байтов, которое работает независимо для каждого байта State и использует таблицу подстановок S. Эта замена включает в себя две операции:
 | [1.1] |
В преобразованиях ShiftRows() байты в последних трех рядах State циклически сдвигаются на разное число байт. Первый ряд (r=0) не сдвигается. Преобразование ShiftRows() осуществляется следующим образом:
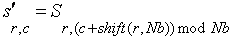 | для 0<r<4 и 0≤c<Nb | [1.3] |
где величина сдвига shift(r,Nb) зависит от номера ряда r следующим образом:
shift(1,4)=1; shift(2,4)=2; shift(3,4)=3
Преобразование MixColumns() обрабатывает State колонка за колонкой, каждая из колонок представляет собой 4-битный код. Колонки рассматриваются как полиномы над полем GF(28). Колонка умножается на фиксированный полином {a}={03}x3+{01}x2+{01}x+ {02} по модулю x4+1 (см. формулу 2а).
В преобразовании AddRoundKey() к State добавляется ключ итерации (Round Key; побитовая операция XOR). Операция производится для каждого байта State.
Ключи итерации вычисляются на основе ключа шифрования с помощью процедуры преобразования ключа (Key expansion). Эта процедура формирует
Nb(Nr+1) слов. Алгоритм требует Nb слов и каждая из Nr итераций требует Nb слов. В результате получается линейный массив 4-байтовых слов, который обозначается
[wi], где i лежит в пределах 0?i Функция SubWord() работает с входными байтами, преобразуя их с помощью S-таблиц. Операция выполняется для каждого из 4 входных
байт. Функция RotWord() использует в качестве входного слова [a0,a1,a2,a3] и возвращает слово [a1,a2,a3,a0]. Рис. 2. Псевдокод реализации процедуры преобразования ключа Все процедуры, описанные в предыдущем разделе, являются обратимыми. Целью дешифровки является обработка зашифрованного массива данных с целью
получения исходного блока данных. Процедуры дешифровки включают в себя функции InvShiftRows(), InvSubBytes(), InvMixColumns() и AddRoundKey().
Псевдокод для процедуры дешифровки представлен на рис. 3. Рис. 3. Псевдокод процедуры дешифровки Процедура InvShiftRows() является обратной по отношению ShiftRows(). Байты в последних трех рядах State циклически сдвигаются
на разное число байт. Первый ряд (r=0) не сдвигается. Преобразование InvSubBytes() является обратной подстановкой байт, в которой S-таблица последовательно применяется для каждого из байтов State. Это достигается за счет обратного аффинного преобразования. Процедура InvMixColumns() является обратной по отношению MixColumns() (см. раздел 1.3). Колонки рассматриваются как полиномы над полем
GF(28). Преобразование AddRoundKey(), описанное в разделе 1.4 является обратимым, так как содержит только операции XOR. В алгоритме дешифровки (рис. 3), последовательность преобразований отличается от порядка операций шифрования, а форма ключей расширения
для шифрования и дешифрования остается неизменной (рис. 4). Однако ряд свойств алгоритма AES допускают формирование эквивалентного кода дешифрования,
где последовательность операций преобразования остается той же самой (с заменой преобразований на обратные). Рис. 4. Псевдокод для эквивалентного обратного преобразования В последнее время появилась новая версия AES-NI (New Instructions) [2], которая позволяет оптимизировать работу алгоритма (понизить загрузку процессора на 50%). Эта версия может использоваться и совместно с SSL. Компания Intel разработала микросхему, реализующую этот алгоритм (серия X5600). Количество клиентов при работе с версией AES-NI может быть увеличено на 13%.
KeyExpansion(byte key[4*Nk], word w[Nb*(Nr+1)], Nk)
begin
word temp
i = 0
while (i < Nk)
w[i] = word(key[4*i], key[4*i+1], key[4*i+2], key[4*i+3])
i = i+1
end while
i = Nk
while (i < Nb * (Nr+1)]
temp = w[i-1]
if (i mod Nk = 0)
temp = SubWord(RotWord(temp)) xor Rcon[i/Nk]
else if (Nk > 6 and i mod Nk = 4)
temp = SubWord(temp)
end if
w[i] = w[i-Nk] xor temp
i = i + 1
end while
end
endРасшифровка
InvCipher(byte in[4*Nb], byte out[4*Nb], word w[Nb*(Nr+1)])
begin byte state[4,Nb]
state = in
AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1])
for round = Nr-1 step -1 downto 1
InvShiftRows(state)
InvSubBytes(state)
AddRoundKey(state, w[round*Nb, (round+1)*Nb-1])
InvMixColumns(state)end for
InvShiftRows(state)
InvSubBytes(state)
AddRoundKey(state, w[0, Nb-1])
out = state
end
Преобразование InvShiftRows()
Преобразование InvSubBytes()
Преобразование InvMixColumns()
Обратное преобразование AddRoundKey()
Эквивалентный код дешифровки
EqInvCipher(byte in[4*Nb], byte out[4*Nb], word dw[Nb*(Nr+1)])
begin
byte state[4,Nb]
state = in
AddRoundKey(state, dw[Nr*Nb, (Nr+1)*Nb-1])
for round = Nr-1 step -1 downto 1
InvSubBytes(state)
InvShiftRows(state)
InvMixColumns(state)
AddRoundKey(state, dw[round*Nb, (round+1)*Nb-1])
end for
InvSubBytes(state)
InvShiftRows(state)
AddRoundKey(state, dw[0, Nb-1])
out = state
end
Для эквивалентной программы дешифровки в конец программы расширения ключа добавляется следующий псевдокод:
for i = 0 step 1 to (Nr+1)*Nb-1
dw[i] = w[i]
end for
for round = 1 step 1 to Nr-1
InvMixColumns(dw[round*Nb, (round+1)*Nb-1])Ссылки
[1]
С.Г. Баричев, В.В. Гончаров, Р.Е. Серов, Основы современной криптографии, 2-е издание, Москва, "Горячая линия - Телеком", 2002
[2]
Advanced Encryption Standard New Instructions
Previous: 6.4.10 Протокол аутентификации Нидхэма-Шредера в случаях симметричной и асимметричной системы шифрования
UP:
6.4 Системы шифрования