6.4 Системы шифрования

История криптографии

Общие требования, предъявляемые к криптосистемам

• Знание использованного алгоритма не должно снижать надежность шифрования.
• Длина зашифрованного текста должна быть равна длине исходного открытого текста (это требование относится к числу желательных и выполняется не всегда).
• Зашифрованный текст не может быть прочтен без знания ключа.
• Каждый ключ из многообразия ключей должен обеспечивать достаточную надежность.
• Изменение длины ключа не должно приводить к изменению алгоритма шифрования.
• Если известен зашифрованный и открытый текст сообщения, то число операций, необходимых для определения ключа, не должно быть меньше полного числа возможных ключей.
• Дешифрование путем перебора всех возможных ключей должно выходить далеко за пределы возможностей современных ЭВМ.
• Если при шифровании в текст вводятся дополнительные биты, то алгоритм их внесения должен быть надежно скрыт.
• Не должно быть легко устанавливаемой зависимости между последовательно используемыми ключами.
• Алгоритм может быть реализован аппаратно.

В симметричных криптосистемах могут использоваться одно- или многоалфавитные подстановки (например, одно-алфавитная подстановка Цезаря), при этом производится замена символов исходного текста на другие с использованием достаточно сложных алгоритмов. Многоалфавитные подстановки несравненно более надежны. К числу простых методов шифрования относится способ перестановок символов исходного текста (этот метод эффективен только лишь при достаточно большой длине исходного текста). Множество перестановок символов для текста из N символов равно N!, что до какой-то степени гарантирует надежность процедуры. Несколько большую надежность предлагает метод гаммирования, когда на исходный текст накладывается псевдослучайная последовательность бит, генерируемая на основе ключа шифрования, например, с использованием операции исключающего ИЛИ. Обратное преобразование (дешифрование) выполняется генерацией точно такой же псевдослучайной последовательности и наложением ее на зашифрованной текст. Гаммирование уязвимо для случая, когда злоумышленнику становится известен фрагмент исходного текста. В этих обстоятельствах он без труда восстановит фрагмент псевдослучайной последовательности, а по нему и всю последовательность. Так если достаточно большое число сообщений начинается со слов "Секретно", а в конце ставится дата сообщения, расшифровка становится вопросом времени и терпения.

Ключ может быть одноразового и многоразового использования. Одноразовый ключ достаточно большой длины (или бесконечный) может обеспечить сколь угодно высокую надежность, но его использование создает неудобства, связанные с его транспортировкой (ключ должен быть как-то доставлен получателю зашифрованного послания). В таблице 6.4.1 приведен пример использования такого вида ключа.

Таблица 6.4.1.

Зашифрованный текст получается здесь из исходного добавлением значения очередного кода ключа (сложение может быть заменено вычитанием или операцией исключающее ИЛИ). Исходный текст в данном случае невозможно восстановить без знания ключа.

Система DES

Наибольшее распространение в последнее время получило блочное шифрование, где последовательность процедур воздействует на блок входного текста. Одним из наиболее известных таких методов стал DES (Data Encryption Standard), который работает с блоками данных по 64 байта (1998 год). Существует четыре режима работы:

Из-за того, что алгоритм DES в настоящее время представляется устаревшим и не обеспечивает достаточной надежности, довольно часто исходный текст последовательно шифруется трижды с помощью различных ключей.

Базовые определения и теоремы

Конгруентность. a конгруентно b по модулю n (a ≡ _nb), если при делении на n a и b, получается идентичный остаток. Так 100 ≡ ₁₁34 (100 и 34 при делении на 11 дают остаток 1) и -6 ≡ ₈10 (ведь -6 =8(-1)+2). Мы всегда имеем a ≡ _nb для некоторого 0 ≤ b≤ n-1. Если a ≡ _nb и с ≡ d, то справедливы равенства:

Аналогичная процедура для деления не всегда справедлива: 6 ≡ ₁₂18 но 3 ≠ 9. Приведенные здесь и далее математические определения и обоснования взяты из: http://lglwww.epfl.ch/~jkienzle/digital/node20.html.

Необходимо также вспомнить о знакомом всем со школьной скамьи понятии наибольшего общего делителя. Для a и b число (a,b) является наибольшим общим делителем, который делит a и b без остатка:

(56,98)=14; (76,190)=38

Теорема 1. Для любых a,b существуют целые числа x,y, для которых ax+by=(a,b). В данной статье не приводится доказательств представленных утверждений, их следует искать в книгах по дискретной математике.

В этом можно убедиться, решая уравнение 30x+69y=3 путем последовательных упрощающих подстановок (ищется целочисленное решение:

30x+69y=3

Легко видеть, что x"=1, y'=0 является решением окончательного уравнения. Мы можем получить решение исходного уравнения путем обратной подстановки.

x'=x"-3y'=1 y=y'-3x'=-3 x=x'-1y=7

Мы можем решить уравнение вида 30x+69y=15 путем умножения нашего решения: y=-15, x=35. Должно быть ясно, что уравнение не будет иметь целочисленного решения, если 15 заменить на что-то некратное (30,69)=3.

Все другие целочисленные решения 30x+69y=15 могут быть получены, варьируя первое решение:

y=-15+(30/3)t x=35 -(69/3)t для целого t

Если мы проделаем то же для произвольного равенства ax+by=(a,b), мы возможно получим один из коэффициентов равным нулю, а другой - (a,b). В действительности эта процедура представляет собой алгоритм Евклида для нахождения наибольшего общего делителя.

Важно то, что этот процесс реализуем на ЭВМ даже в случае, когда a и b имеют несколько сотен значащих цифр. Легко показать, что 600-значное число не потребует более чем 4000 уравнений. Теорема 1 справедлива и для простых чисел.

Во многих криптографических приложениях используется:

a a² a³ … mod p, где a и p целые числа.

Оказывается, можно выполнить такие вычисления даже для случая, когда в указанную процедуру вовлечены достаточно большие числа, например:

Фокус заключается в том, что берется число и осуществляется возведение в квадрат.

432² = 186624; 186624 mod 987 = 81; 432⁴ mod 987 = 81² mod 987 = 639
432⁸ -> 639² mod 987 -> 690 …. 432⁵¹² -> 858
так как 678= 512+128+32+4+2, то:
432⁶⁷⁸->(81)(639)….(858) -> 204

Вычисления с использованием показателя включают в себя ограниченное число умножений. Если числа содержат несколько сотен цифр, необходимы специальные подпрограммы для выполнения таких вычислений. Рассмотрим последовательность степеней 2ⁿ mod 11:

2 4 8 5 10 9 7 3 6 1

Здесь числа от 1 до 10 появляются в виде псевдослучайной последовательности.

Теорема 2

Пусть p является простым числом. Существует такое a, что для каждого 1≤ b ≤ p-1, существует такое 1≤ x ≤ p-1, что a^x ≡ _pb, a не обязательно равно 2.

Степени 2 mod 7 равны 2, 4, 1. Далее числа повторяются, а числа 3, 5, или 6 не могут быть получены никогда. Рассмотрим некоторые следствия этой теоремы.

Следствие 4. Пусть a соответствует требованиям теоремы 2, тогда a^p-1 ≡ _p1.

Следствие 5. Для любого b ≠ 0, b^p-1 ≡ _p1.

Следствие 6. Если x ≡ _(p-1)y, тогда b^x ≡ _pb^y

Пусть b ≠ 0, d наименьшее положительное число, такое что b^d ≡ _p1. Тогда для любого с>0 c b^c ≡ _p1 d делит c без остатка. В частности для следствия 5, d делит p-1 без остатка.

Согласно теореме 2, если p простое число, существует такое a, при котором равенство a^x ≡ _pb имеет решение для любого b ≠ 0. Такое значение a называется примитивным корнем p, а x называется дискретным логарифмом b. Получение b при заданных a и x относительно просто, определение же x по a и b заметно сложнее. Многие современные системы шифрования основываются на факте, что никаких эффективных путей вычисления дискретных логарифмов не найдено. Никакого эффективного метода определения примитивных корней также неизвестно. Однако часто возможно найти примитивные корни в некоторых специальных случаях. Возьмем p=1223. p-1=2*13*47. Согласно лемме, если a не примитивный корень, тогда мы либо имеем a²⁶, a⁹⁴ или
a⁶¹¹ ≡ ₁₂₂₃1. a=2 и a=3 не годятся, но a=5 соответствует всем трем условиям, таким образом, это значение является примитивным корнем. Мы могли бы сказать, что a=4 не может быть признано примитивным корнем без проверки.

Легко показать, что если a примитивный корень, a^x примитивный корень в том и только том случае, если (x,p-1)=1. В этом примере это означает, что число примитивных корней равно

1222*(1/2)*(12/13)*(46/47)=552

Таким образом, если мы выберем а произвольно, вероятность того, что это будет примитивный корень равна ~.45. Выбирая а наугад и тестируя, можно сравнительно быстро найти примитивный корень.

Наиболее современные системы шифрования используют асимметричные алгоритмы с открытым и секретным ключами, где нет проблемы безопасной транспортировки ключа. К числу таких систем относится алгоритм rsa (rivest-shamir-adleman - разработчики этой системы - Рональд Ривест, Ади Шамир и Леонард Адлеман, 1977 год), базирующийся на разложение больших чисел на множители.

Другие сходные алгоритмы используют целочисленные логарифмы, элиптические кривые (считается одним из наиболее криптографически прочных) и вычисление корней уравнений. В отличие от других систем эти позволяют кроме шифрования эффективно идентифицировать отправителя (электронная подпись). К системам с открытым ключом предъявляются следующие требования:

• шифрованный текст трудно (практически невозможно) расшифровать с использованием открытого ключа.
• установление закрытого ключа на основе известного открытого должно быть нереализуемой задачей на современных ЭВМ. При этом должна существовать объективная оценка нижнего предела числа операций, необходимых для решения такой задачи.

К сожалению, эти алгоритмы достаточно медленно работают. По этой причине они могут использоваться для транспортировки секретных ключей при одном из традиционных методов шифрования-дешифрования.

Но следует помнить, что не существует абсолютных мер защиты. На рис.6.4.1. показан способ нарушения конфиденциальности в системах с двухключевой схемой шифрования.

Рис. 6.4.1.

Если хакер умудрится вставить свою ЭВМ в разрыв канала, соединяющего субъектов А и В, у него появляется возможность перехватывать в том числе и шифрованные сообщения. Пусть субъект А сформировал пару ключей К_1А и К_2А (ключ с индексом 2 является секретным), аналогичную пару ключей сгенерировал субъект В (К_1В и К_2В). Хакер же тем временем подготовил две пары ключей (К_1ХА:К_2ХА и К_1ХВ:К_2ХВ). Когда субъект А пошлет открытый ключ К_1А субъекту В, хакер его подменит ключом К_1ХА. Аналогичную процедуру он проделает с ключом К_1В, посланным от В к А. Теперь сообщение А к В, зашифрованное с помощью ключа К_1ХА будет послано В. Хакер его перехватывает, дешифрует с помощью ключа К_2ХА, шифрует с помощью ключа К_1ХВ и посылает В. Субъект В, получив послание, дешифрует его с помощью "секретного" ключа К_2ХВ, полученного от хакера (о чем он, естественно, не подозревает). Аналогичная процедура будет проведена и при посылки сообщения от В к А. В сущности единственным параметром который изменится существенным образом будет время доставки сообщения, так как это время будет включать дешифровку и повторную шифровку сообщения. Но при использовании быстродействующей ЭВМ и при работе с традиционной электронной почтой это может оказаться незаметным. Понятно, что между А и В появится дополнительный шаг (hop). Но и это может быть легко замаскировано под прокси сервер или Firewall.

Начиная с 1997 года NIST (National Institute for Standards and Technology) совместно с промышленностью и криптографическим сообществом разрабатывал приемника для алгоритма DES (длина ключа 56 бит). В результате был создан алгоритм AES (Advanced Encryption Standard), который был опубликован в 2001 году (FIPS 197). AES представляет собой блочный, симметричный алгоритм шифрования с длиной блока 128 бит. Длина ключа может принимать значения 128, 192 или 256 бит (AES-128, AES-192 и AES-256, соответственно). Если предположить, что ключ DES можно подобрать за секунду, то для подбора ключа AES-128 потребуется около 149 триллионов лет (кстати, возраст нашей вселенной всего 20 миллиардов лет). Кроме AES ISO/IEC 18033 (см. http://www.ni.dm.de, http://csrc.nist.gov и www.x9.org) специфицирует еще шесть различных блочных шифров (см. таблицу ниже).

Базовые характеристики блочных алгоритмов шифрования представлены в таблице ниже (смотри http://book.itep.ru/6/idea_647.htm, ~6/des_641.htm и ~6/safr_648.htm).

Относительные уровни безопасности разных алгоритмов представлены ниже.

Стандарт на хэш функции задает документ ISO/IEC 10118. К сожалению, не существует международного стандарта для управления информационными системами безопасности.Стандарт на хэш функции задает документ ISO/IEC 10118. Эти хэш функции (см. табл. 19.5) используются практически во всех видах электронных подписей (ISO/IEC 14888). К сожалению, не существует международного стандарта для управления информационными системами безопасности.

В настоящее время имеется три семейства криптосистем с открытым ключом.

1. Системы IF (Integer Factorization - целочисленная факторизация), такие как система цифровой подписи, базирующаяся на RSA, использует сложность факторизации при работе с большими целыми числами.
2. Системы DL (Discrete Logarithm - целочисленный логарифм), такие как алгоритм цифровой подписи NIST (DSA, FIPS 186), базируются на вычислительной сложности оперирования с целочисленными логарифмами.
3. Системы EC (Elliptic Curve эллиптические кривые) являются сходными с DL примитивами. Они основываются на вычислительной сложности проблемы расчета целочисленных логарифмов через эллиптические кривые. Преимуществом этой системы является относительная ее сила по отношению к длине параметра. Другими словами эллиптические кривые предоставляют большую секретность на бит. Примером эллиптической кривой является уравнение типа Y²=X³ +aX+b.

Прочность всех этих алгоритмов основывается на трудностях, например, разложения больших чисел на сомножители или работы с целочисленными логарифмами. До сих пор не доказано, что не существует алгоритмов быстрого решения указанных проблем. Если такие алгоритмы будут найдены, придется придумывать другие системы шифрования. Следует также помнить, что в случае взлома машины, криптографические методы окажутся бесполезными, так как, например spyware, сможет иметь доступ к исходному тексту файлов или вводимых паролей.

Развитие методов программирования и повышение быстродействия ЭВМ приводит к понижению надежности систем шифрования. Симметричные шифры теряют один бит безопасности в год. Хэш-функции и схемы, основанные на эллиптических кривых (ISO/IEC 15946-2), теряют два бит безопасности в год. RSA-схемы теряют 30 бит безопасности в год. На рис. 6.4.2. показана временная зависимость деградации безопасности шифров (см. Network Security, V2004, Issue 12, декабрь 2004, стр. 6-11).

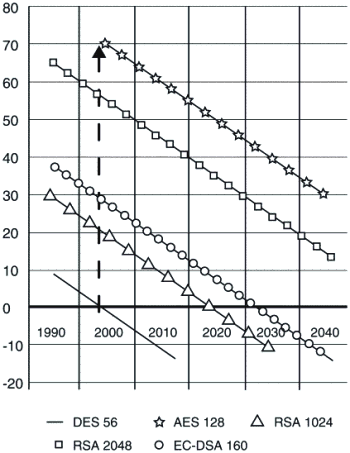
Рис. 6.4.2. Время жизни криптографических алгоритмов

Для взлома паролей и подбора крипто-ключей могут использоваться botnet (сети, состоящие из взломанных машин). Ведь размеры таких сетей достигает нескольких миллионов, в 2009 году поставлен рекорд в 10.000.000. За год взламывается более 100.000.000 машин.

Полезную информацию по системам шифрования можно получить на следующих серверах: